Michael La Croix
![[Picture of Me]](thumbs/Hiking.jpg)
Contact Me
Office: E18-458
Email: malacroi (@math.mit.edu)
I am a postdoctoral associate in the
Applied Mathematics department at the
Massachusettes Institute of
Technology, where I am currently studying random matrices under
the supervision of Professor
Alan Edelman. My
current research is motivated by the interplay between the
combinatorics of topological maps and the statistics of random
matrices with independent Gaussian entries. This is a natural
extension of work on enumerative combinatorics that I completed during
my Doctoral studies as a student of Professor
David Jackson
and later also Professor
Ian Goulden, in
the Combinatorics
and Optimization department at the
University of Waterloo.
Here is a recent CV.
I was previously a lecturer in the department of
Statistics and
Actuarial Science at
the University of Waterloo,
where I spent 16 months co-ordinating an introductory course in
probability aimed at honours Mathematics students. The structure of
the course was such that many students attended lectures via
video-conferencing, or by watching recordings of lectures, and a major
component of my duties consisted of adapting the course to make it
more suitable for consumption in this format.
Random Matices and Combinatorics
In my PhD thesis, I introduced a
combinatorial model for a map generating series defined algebraically
in terms of Jack symmetric functions. Polynomials associated with
this generating series also appeared in moment calculations
Professor Alan Edelman
performed while studying the Gaussian β-ensemble, and we have
been working to expose the connection to a broader audience.
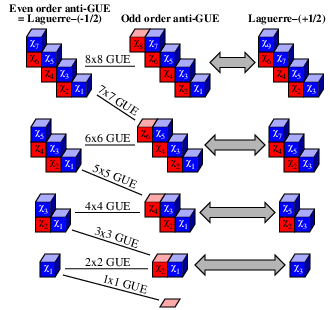
Generalizations of this model can also be used to provide
combinatorial interpretations to the moments of β-Hermite and
β-Laguerre matrix ensembles, and I am in the process of preparing
illustrated notes that explore these connections. In the particular
cases of β=1 and β=2, corresponding to real matrices and
complex matrices, the link between combinatorics and random matrices
can be made even more explicit, and provides an analytic framework for
studying questions about the center of the group algebra of the
symmetric group and the double coset algebra of the hyper-octahedral
group.
One of the problems motivating the creation of Jackson and Visentin's
An Atlas of the Smaller Maps in Orientable and Nonorientable Surfaces
is the existence of a functional equation relating the generating
series of several different classes of oriented combinatorial maps
(their so-called q-Conjecture). This identity can be
interpreted as an identity between the distributions of singular
values of two different classes of Gaussian random matrices, and this
provides a common framework for explaining several different
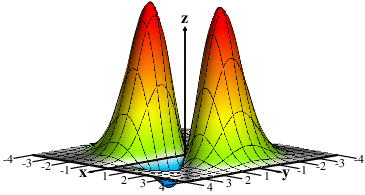
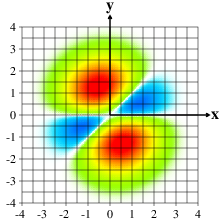
properites that nominally involve the eigenvalues of GUE matrices.
The implications are explored in
"The Singular Values of the
GUE (Less is More)". A follow-up,
"The Singular Values of the
GOE" identifies analogous properties of the GOE, although the
combinatorial link is less evident in this setting.
Typesetting Math
The standard medium for typesetting math is LaTeX.
If you're interested in learning LaTeX, a good place
to start is
The Not So Short Introduction to LaTeX 2e.
Further information on math specific issues, and
on using AMS-LaTeX, can be found in the
Short Math Guide For LaTeX.
As an example, here is the
LaTeX Source
source for the main file of my Master's essay
on "Approaches to the Enumerative Theory of
Meanders". The main file reveals all the macros
I used, and shows the general structure of
a LaTeX document. Here is the finished
product for comparison.
My interests in typesetting extend to a professional level. I am the
author of LaTeX classes to control page layout of user submissions to
an online economics journal, Review
of Economic Analysis, and also designed the class used for
course notes for core-courses for math majors at the University of
Waterloo.
Photography
Prior to becoming interested in digital imaging, I spent a lot of
time dabbling in exotic photography techniques.
-
These represent the results of a project
to create double-exposure
 Red/Blue 3D Photographs
directly on film.
Red/Blue 3D Photographs
directly on film.
-
I am also facinated by the colors present
in low-light settings. A
 selection of photographs shows
the color of stars and illustrates the daylight spectrum
available under the light of a full moon.
selection of photographs shows
the color of stars and illustrates the daylight spectrum
available under the light of a full moon.
![[Picture of Me]](thumbs/Hiking.jpg)















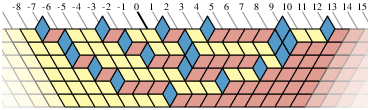
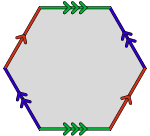
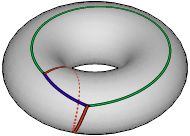
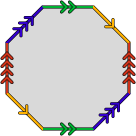
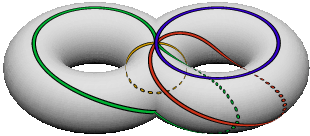
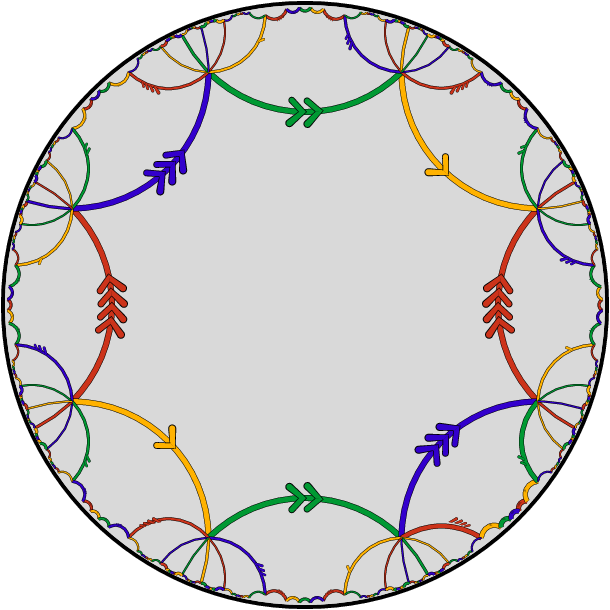
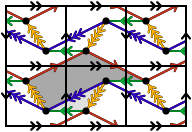


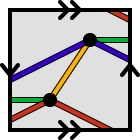


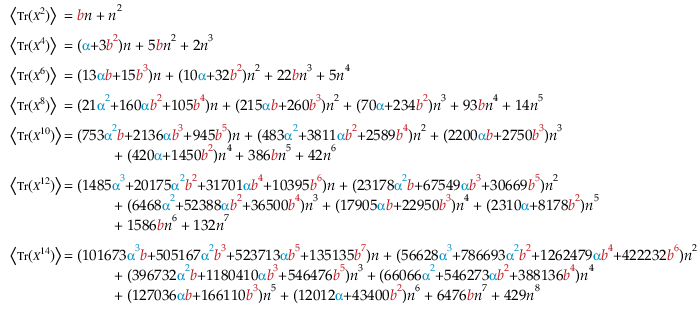
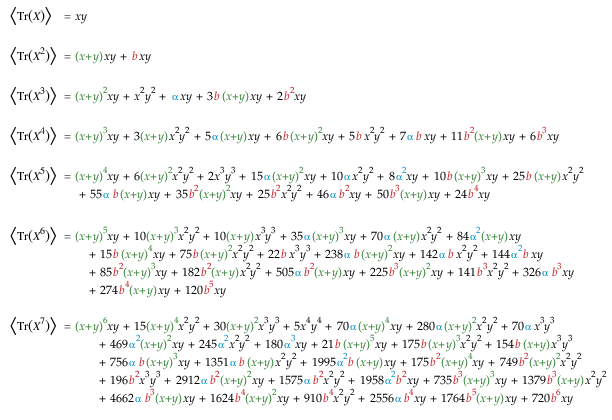







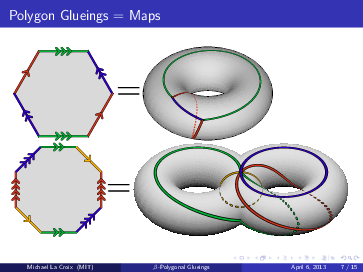 β–ensembles from polygon glueings
β–ensembles from polygon glueings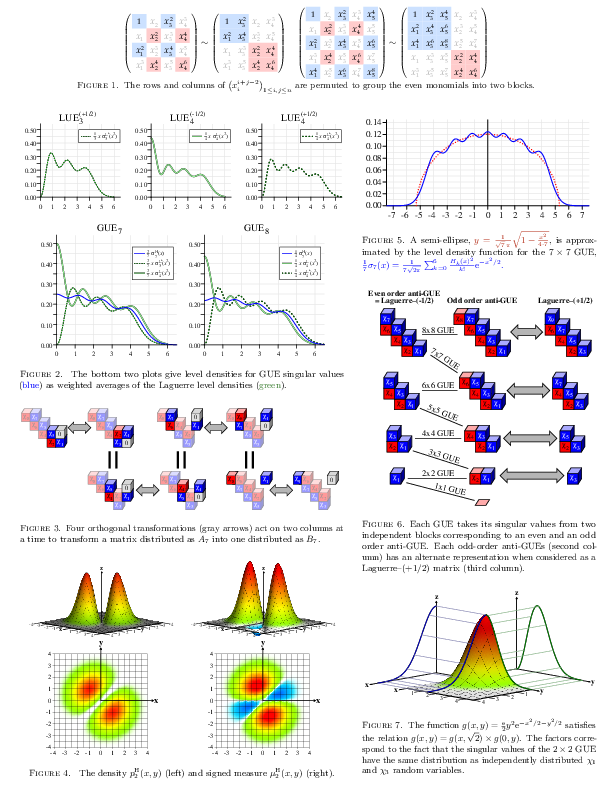 A handout about the GUE
A handout about the GUE
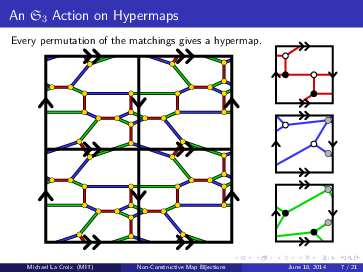 Non-constructive bijections
Non-constructive bijections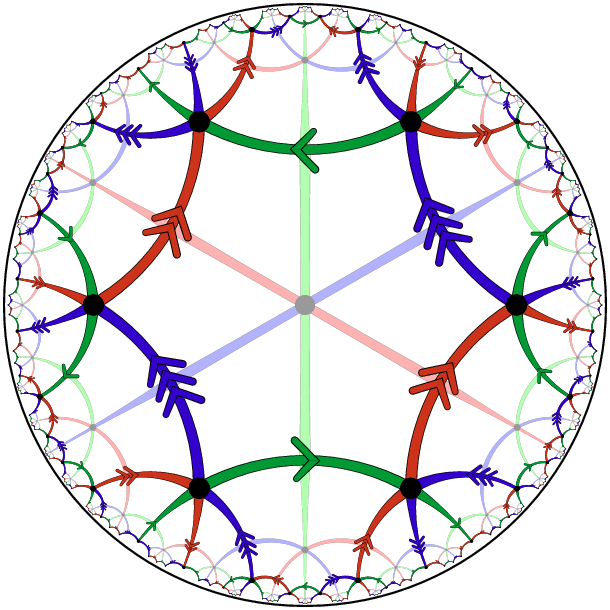 Non-Orientability and Jack Symmetric Functions
Non-Orientability and Jack Symmetric Functions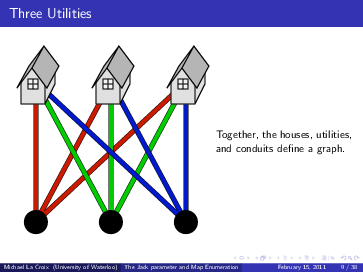 What is Map Enumeration?
What is Map Enumeration?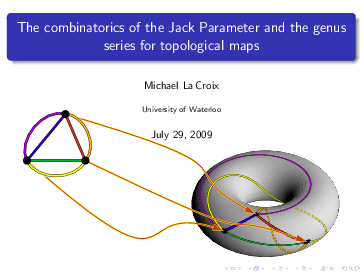 PhD Defence
PhD Defence
 Q-Conjecture
Q-Conjecture
 2nd Stage Exam
2nd Stage Exam Meanders
Meanders
 Rubik's Cube
Rubik's Cube
