Math 247, Winter 2007
Instructor:
Nico Spronk
Class Time and Place: 8:30-9:20 MWF (sorry!) in MC 4044.
Recommended text: We are using the Math 217-317
Lecture Notes (.pdf) produced by
Volker Runde at the University of Alberta.
I will arrange to have these copied and coil-bound to be sold, at cost,
as Math 247 Lecture Notes at Pixel Planet (MC 2018).
There is an interesting, though extremely compact, book
Calculus on Manifolds by Michael Spivak, 1965 Addison Wesley,
Reading MA, which might be a recommendable supplement.
Also interesting, and less compact,
is the book Advanced Calculus by Gerald B. Folland,
2002 Prentice-Hall, Upper Saddle River NJ. Do note that neither of these
books cover all of the topics we will need, but they each cover other topics
which go beyond the scope of Math 247.
Office hours: TBA
Information sheet (.pdf)
Syllabus (.pdf)
Homework assignments: All files are PDF.
Assignment #1
Sample solutions
Assignment #2
Sample solutions
Assignment #3
Sample solutions
Assignment #4
Sample solutions
Assignment #5
Sample solutions
BONUS QUESTION: Find a compact set A in the real line which is
its own boundary and does not have content zero. Deduce that there
exists a compact connected subset of R^2 which does not have Jordan content.
Assignment #6
Sample solutions
Problem set on Implicit Function Theorem and Lagrange Multipliers.
Sample solutions Notes: for question 2 (b) it is better not to use
the DE. Unfortunately, I did not get around to the 2-constraint
Lagrange multiplier theorem; I do not know how to do 7 (a) with
only one constraint.
Final Exam: Monday, April 16, 4:00-6:30pm in PAC 6.
See the Winter 2007
exam schedule (PDF).
Special Office Hours: Friday, April 13, 2-5PM.
Graded assignments may be found in wooden box beside my office door.
A function which is partially differentiable but not differentiable:
In Maple enter
> f:=(x,y)->x*y/(x^2+y^2);
> plot3d(f(x,y),x=-1..1,y=-1..1,axes=boxed);
to obtain
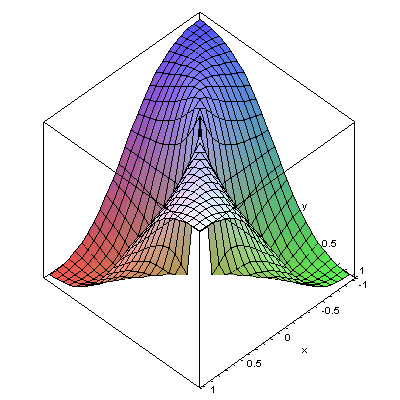
It should be clear from the picture, that no tangent plane
could be placed at (0,0).
Here's another one. In Maple enter
> g:=(x,y)->x^2*y/(x^4+y^2);
> plot3d(g(x,y),x=-0.01..0.01,y=-0.01..0.01,axes=boxed);
to obtain
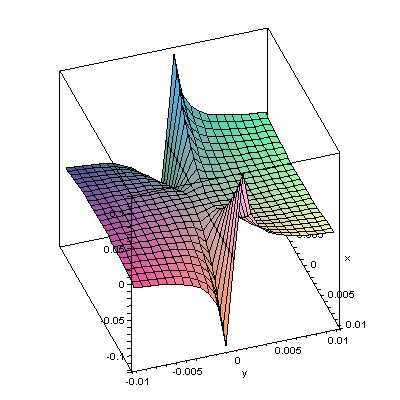
With a little imagination, you can see why the derictional derivatives
admit the strange formula of Assignment #4. The picture doesn't quite
convincingly conclude that the tangent plane does not exist at (0,0).
However, you'll
obtain a comaparbale picture if you continue to zoom in. This suggests
that the tangent plane cannot exist (while the mathematics confirms it).
Supplement to Appendix in Lecture Notes:
An easy to compute
characterisation of positive definite matricies.

