M. Match mental models

The designer has a certain model for interactive statistical analysis in mind

  

Figure: Matching mental models.

which he/she tries to capture in the design. This design is then implemented as a working system (see Figure ). The user too has a model for an interactive statistical analysis in mind. Working with a particular system forces the user to construct a working model of that system, which can be quite different from both his/her general mental model and that of the designer. The only communication between the mental models of the user and the designer is through the implemented system.

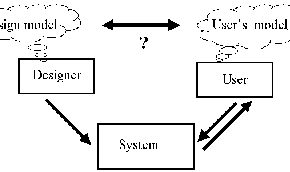
Ideally these two models should match and the system implementation should follow them closely. The system would then be more immediately useful to the analyst. Moreover, it would be more easily extended to new areas by the user; the step from user to designer would be small.

To better match models, Norman (1988) recommends the designer:

1.

Use existing common knowledge,

2.

Communicate the model,

3.

Use the model, and

4.

Reinforce the model.

There are two types of existing knowledge common between the designer and the user of a statistical analysis system. The first is the everyday sort such as switches, push-buttons, dials, and gauges which can be mimicked to good effect in a visual display. The familiarity of the visual representation makes its use obvious to the user.

The second is the knowledge about statistical analysis which, although specialized, is shared by both user and designer. In the early command line systems this was evident primarily in the names of commands. In early direct manipulation interfaces, it is first evident through common interactive statistical graphics.

Strictly speaking, it is not necessary to make maximal use of the existing common knowledge. If the designer is successful in communicating, using, and reinforcing the model then the user can be trained to adopt it. In the extreme, a user who learned about statistical analysis solely by interacting with a single statistical system might very well have a mental model essentially coincident with that of the designer. When computational resources are scarce this is particularly desirable.

Ever faster processors and cheaper memory means that we can now afford to devote more resources to system software which better models existing statistical knowledge. Matching fundamental system components directly to the basic structures of statistical analysis maximizes use of the specialized knowledge common between designer and user.

This approach has important consequences. First, communicating the system model to a statistically trained user should be straightforward. Second, the designer writing code in terms of these fundamental components is actively exercising the model and providing the user with easily understood means to tailor the system to his/her needs. Third, such use reinforces the model.

Not surprisingly, there is abundant structure in statistical knowledge relevant to interactive analysis. Many statistical concepts are quite naturally represented as data structures, for example:

• Datasets, variates, cases, ...
• Random variates, parameters, likelihoods, ...
• Response models, linear models, smooths, ...
• Fitted models, estimates, ...
• Borel Sets, measures, probability measures, ...
• Mathematical functions, survivor functions, state transition intensity functions ...

Object-oriented programming seems to be particularly well-suited to modelling these concepts. Classes are used for each of these structures with inheritance hierarchies which follow the so-called `IS-A' relations as in a cauchy distribution IS A student distribution with one degree of freedom and hence the class cauchy-distribution appears as a sub-class of the student-distribution class. The reasoning is that a user who has an instance of a cauchy-distribution should expect the same functionality from it as any other instance of a student-distribution with some behaviour specialized (e.g. moment calculations). In this way the known relations between statistical concepts is modelled by the definition of the classes and class hierarchies.

Generic functions and specialized methods are also useful in modelling statistical concepts which might not be represented in a hierarchy. In Quail for example, the generic function random-value applies equally to any instance of a distribution and to any dataset. This is so that the user may regard the dataset as an empirical distribution, as in resampling procedures, without changing its class to some kind of distribution.

  

Figure: A typical screen shot from Quail.

Nothing about matching mental models is directed exclusively at either programming language interfaces or at direct manipulation interfaces but rather is directed at both. The fact that so many statistical concepts can be directly modelled as data structures has an important consequence for this approach. Namely, graphical user interfaces can be built by laying out visual displays of the statistical objects themselves - direct manipulation and programmatic or command line interfaces use the same structures as arguments. The information relevant to both is stored within the object so that the transition between the two interface styles is relatively straightforward.

In Quail this is accomplished by having every graphic component maintain a pointer to the relevant statistical object being displayed - this is its viewed object (e.g. see Hurley and Oldford, 1991). A fitted line, for example, would have a pointer to the fit-object which it visually represents in a plot. Conversely, every statistical object in Quail returns a graphics object when asked for its display (see Oldford, 1998, 1997 for more discussion).