



Math Encounters, August 4, 2021
National Musuem of Mathematics

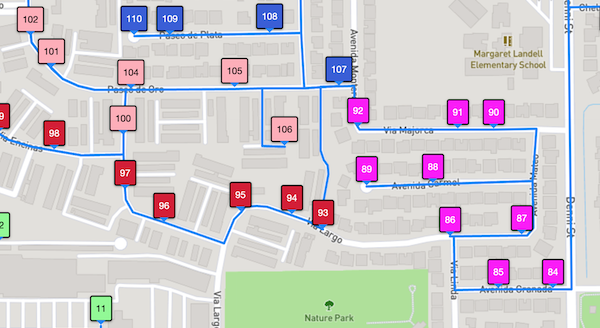
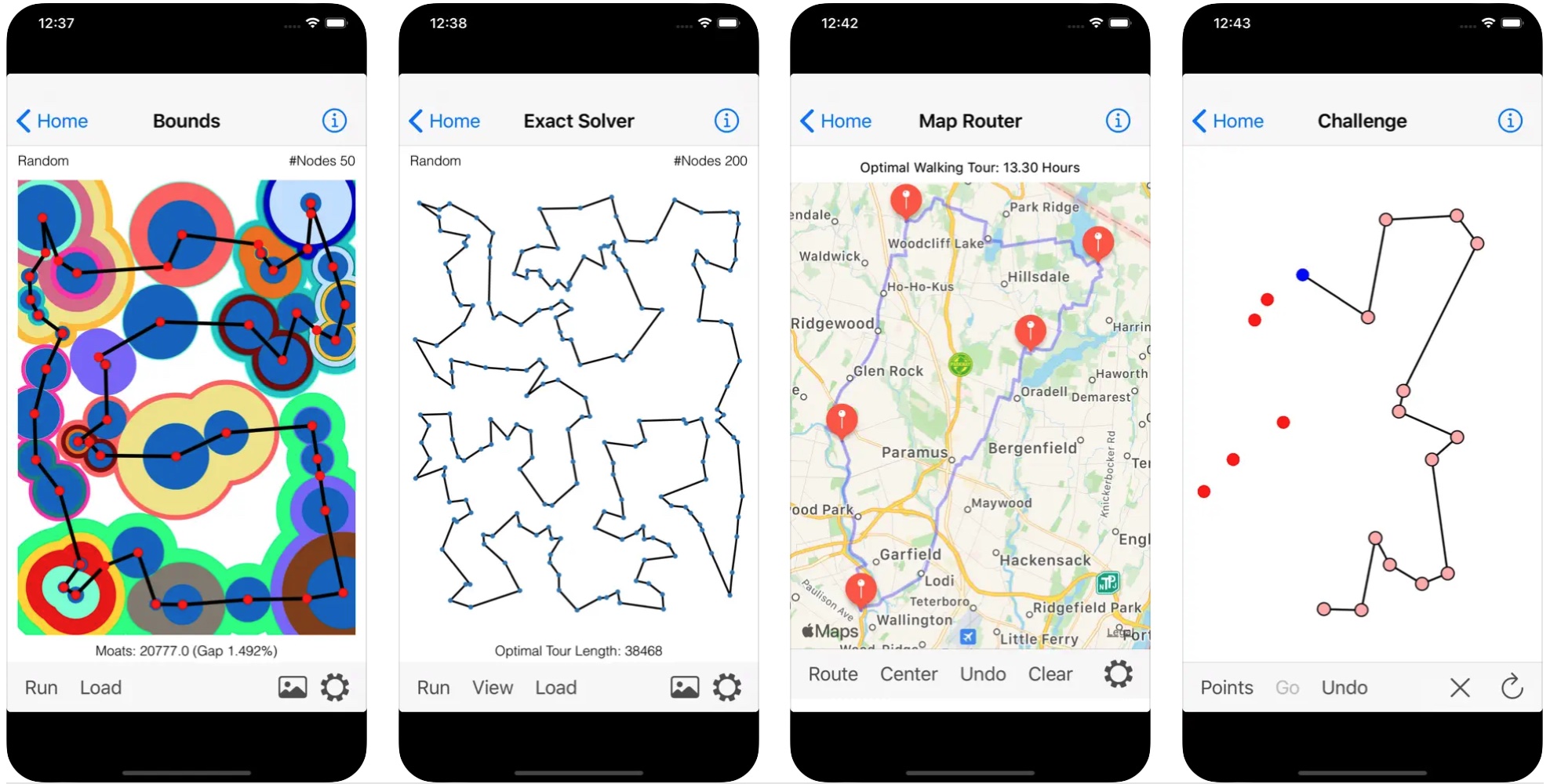
Web app for learning/teaching TSP solution methods.
The Traveling Salesman Problem, or TSP for short, is one of the most intensively studied problems in computational mathematics. These pages are devoted to the history, applications, and current research of this challenge of finding the shortest route visiting each member of a collection of locations and returning to your starting point.
 |

|
 |

|
 |
Math Encounters, August 4, 2021 National Musuem of Mathematics |
 |
Traveling Salesman Problem DIY Web app for learning/teaching TSP solution methods. |
 |
|
 |
|
 |
Winning $100,000 in the Amazon Last Mile Routing Research Challenge. |  |
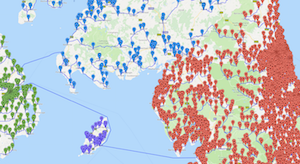
How to visit 1.33 billion stars. |
 |
|
 |
|
 |
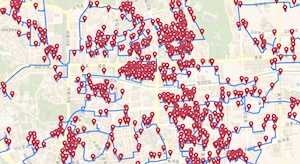
Walking to 81,998 Korean bars. |  |
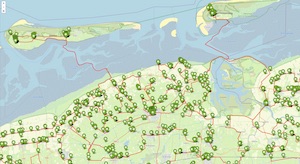
Cycling tour to 57,912 Dutch monuments. |
 |
|
 |
TSP app for iPhone/iPad/Mac Concorde available on the Apple App Store. It's free! |
 |

|
 |
|
 |
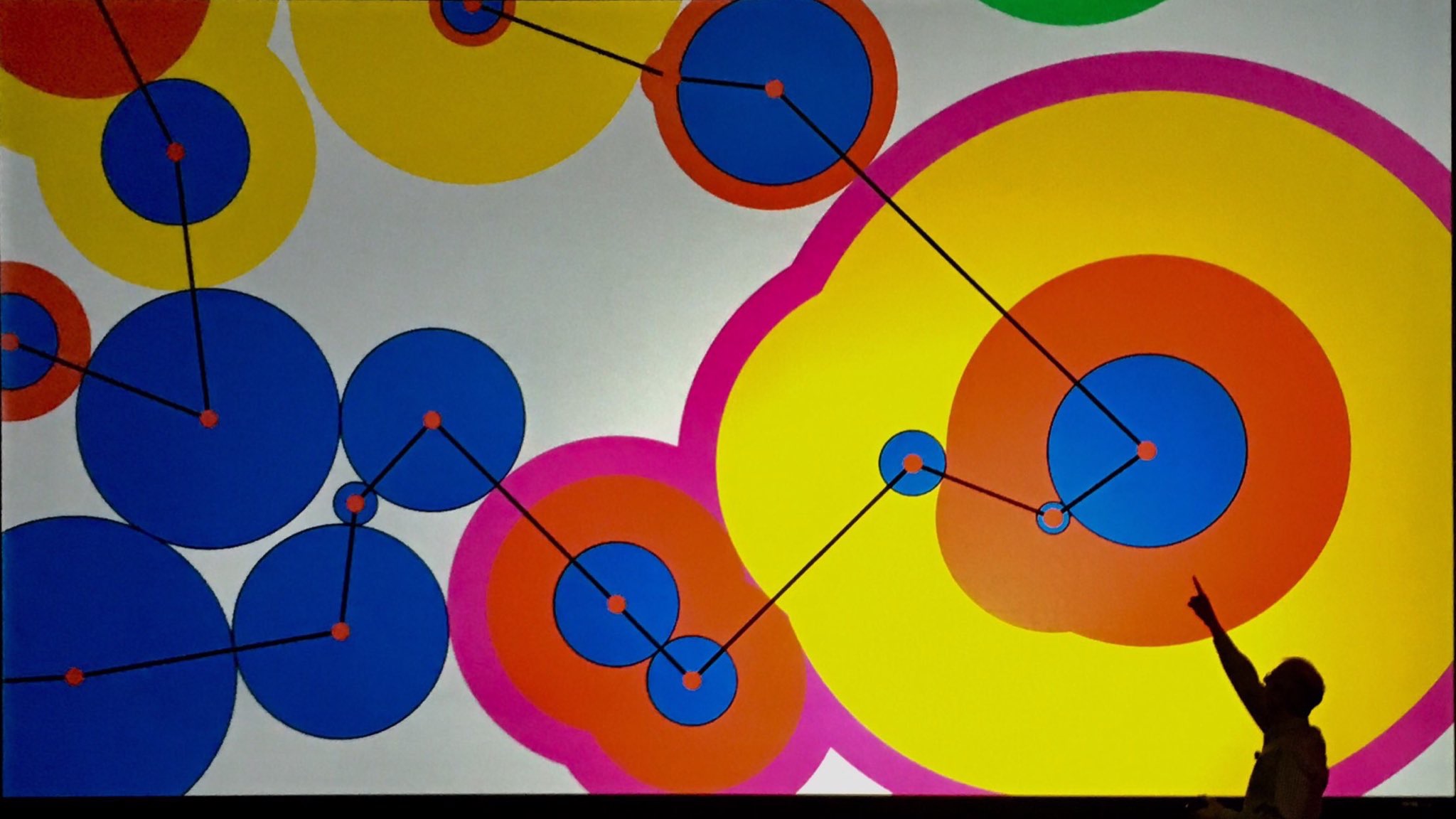
IFORS Distinguished Lecture EURO 2019, Dublin |
 |
MAA Invited Address 2018 Joint Math Meetings |
 |
|
 |
|
 |
Optimal crawl to 49,687 pubs in the UK. |  |
Visit 49,603 historic sites in the US. |
| TSP Tutorial in Python |
 |
Nice intro to the TSP by Peter Norvig | |
| Cutting-plane method |  |
YouTube video (in Siri's voice) | |
| Pokemon Go Tours |
 |
Shortest routes to Catch 'em All | |
| Tour for Extra Milers |
 |
Drive to all 3100 US county seats | |
| Queen of College Tours |
 |
Optimal road trip to visit 647 colleges | |
| Hiking Tour of Austria |
 |
Get a view of 100 mountain peaks | |
| Scientific American |
 |
Short piece on Yogi Berra and the TSP | |
| Travelling Salesman |
 |
Thriller movie centered around a solution of the TSP | |
| Mona Lisa TSP |
 |
$1,000 Prize for a 100,000-city challenge problem. | |
| pla85900 |
 |
Solution of a 85,900-city TSP. | |
| Iowa Tour |
 |
Optimal route for a 99-county campaign tour. |
 |
|
|
 |
|
 |
 |
 |
 |
![]()
The work described here is supported by the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Department of Combinatorics and Optimization at the University of Waterloo.
Contact: William Cook (bico@uwaterloo.ca)