How can we know that our tour is good (or best) when compared to all of the other tours that we have not considered? One simple answer it to just consider all possible tours, but, like many other similar problems, the number of tours grows so quickly that directly checking all of them for a modest-size instance, say 30 cities, is well beyond the capabilities of even the fastest of today's super-computers. What we need are more subtle way to make conclusions about the lengths of all tours through a set of points.

In other words, we need methods that allow us to make valid statements of the form "No tour through this set of points can have length less than 100" where we would replace 100 by a suitable length B for the given TSP instance. Such a number B is called a lower bound for the TSP since it bounds from below the length of our tours.

There are a number of different strategies for finding good lower bounds for the TSP. In Concorde and other modern TSP solvers, the bounding technique of choice goes back to G. Dantzig, R. Fulkerson, and S. Johnson and is based on the solvabilty of mathematical models known as linear programming problems. We will introduce the Dantzig-Fulkerson-Johnson idea by using a geometric interpretation that was described by M. Juenger and W. R. Pulleyblank in the 1980s.

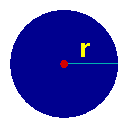
Let us suppose our TSP consists of a set of points in the plane and that the cost to travel between two cities is the (Euclidean) distance between the corresponding points. To begin, we draw a disk of radius r centered at city 1 in such a way that the disk does not touch any of the other cities. Juenger and Pulleyblank call such a disk a control zone.

Now the salesman must at some point in his/her tour visit city 1 and to do so they will need to travel at least distance r to arrive at the city and at least distance r to leave the city (since each other city is at least distance r from city 1). We can conclude that every tour has length at least 2r, that is, we can set B = 2r and have a lower bound for this TSP instance.

When judging a lower bound, bigger is better. Unfortunately, for almost any TSP you can think of, the bound 2r will be rather small when compared to the length of any tour through the points. But the answer is simple, we can draw a seperate disk for each of our cities, as long as the disks do not overlap. In this we way we get twice the sum of the radii of the disks as a lower bound for the TSP.

Since we have many cities, it is convenient to have a name for the radius of each of the disks we are creating. There seems no way around introducing a bit of standard mathematical notation, so for each city i let us denote by r_i the radius of its disk.

If we have five cities, as in the following figure, then by specifying values for each of the five radii r₁ r₂ r₃ r₄ r₅ we can obtain a lower bound for the TSP.

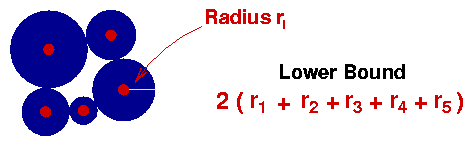
Since we want the bound to be as large as possible, we would like to choose the five radii so as to maximize twice their sum subject to the condition that the disks do not overlap.

The non-overlapping condition can be expressed succiently as follows. For a pair of cities i and j, let dist(i,j) denote the distance from i to j. To ensure that the disks for i and j do not overlap, we must choose the radii so that

r_i + r_j <= dist(i,j)

that is, the sum of the two radii can be at most the distance beteeen the cities.

Putting everything together, the problem of getting the best TSP bound from our collection of disks can be written as follows.

Maximize 2r₁ + 2r₂ + 2r₃ + 2r₄ + 2r₅

Subject To

r₁ + r₂ <= dist(1,2)

r₁ + r₃ <= dist(1,3)

r₁ + r₄ <= dist(1,4)

r₁ + r₅ <= dist(1,5)

r₂ + r₃ <= dist(2,3)

r₂ + r₄ <= dist(2,4)

r₂ + r₅ <= dist(2,5)

r₃ + r₃ <= dist(3,4)

r₃ + r₃ <= dist(3,5)

r₄ + r₅ <= dist(4,5)

r₁ >= 0, r₂ >= 0, r₃ >= 0, r₄ >= 0, r₅ >= 0

This is an example of a linear programming (LP) problem. The important features are that we are maximizing a weighted sum of some unknown quantites (in our case the radii of the disks), subject to constaints that can be expressed as various weighted sums being at most or at least some specfied values (in our case the non-overlapping constraints and the condition that no disk should not have a negative radius).

Linear programming is a very important mathematical model, having far-reaching applications. An important feature of LP models is that even very large ones (with over a million unknown values) can be solved efficiently with a variety of new and old solution methods.

In the context of the TSP, the most important of these solution techniques is the one created by George Dantzig (the same Dantzig as in the DF&J work) in the 1940s. Dantzig's solution technique is known as the simplex method and is used in many of the state-of-the-art LP solvers available today. In 2000, the simplex method was named as one of Top 10 Algorithms of the Century.

Getting back to our disk lower bound, we can employ the simplex method to easily get the best choices for the radii for instances with up to 1,000 cities or more. As we get much larger than 1,000 cities, the number of constraints we need to enforce the non-overlapping condition (it is 450,000 if we have 1,000 cities) begins to make the LPs a challenge to solve directly, but the difficulties can be overcome and we will comment on this later.

A more pressing problem however is that the quality of the bound we get from the best collection of disks is often not all that great. The nice packing of disks in the 5-city figure given above is a bit misleading -- usually the bound we get from the best packing is significantly below the length of the best tour. An example of what can go wrong is given in the figure below.

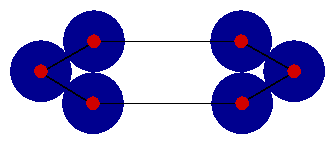
The trouble is that the disks bump into each other and cannot cross the gap between the two clusters of three cities. To improve our lower bound, we will add in a structure that allows us to take advantage of the fact that we know any tour must cross the gap at least twice. This is discussed in the Subtour Elimination page.