A breakthrough in solution methods for the traveling salesman problem (TSP) came in 1954, when George Dantzig, Ray Fulkerson, and Selmer Johnson [2] published a description of a method for solving the TSP and illustrated the power of this method by solving an instance with 49 cities, an impressive size at that time. Riding the wave of excitement over the numerous applications of the simplex method (designed by George Dantzig in 1947), they attacked the salesman with linear programming as follows.

Each TSP instance with  n  cities can be specified as a vector of length  n(n-1)/2  (whose components, indexed by the edges of the complete graph, specify the costs) and each tour through the  n  cities can be represented as its incidence vector of length  n(n-1)/2  (with each component set at 1 if the corresponding edge is a part of the tour, and set at 0 otherwise); if $c^T$ denotes the cost vector (thought of as a row vector) and if ${\cal S}$ denotes the set of the incidence vectors (thought of as column vectors) of all the tours, then the problem is to

\begin{displaymath}{ } \mbox{ minimize } c^Tx \mbox{ subject to } x\in {\cal S}. \end{displaymath} (0.1)

Like the man searching for his lost wallet not in the dark alley where he actually dropped it, but under a streetlamp where he can see, Dantzig, Fulkerson and Johnson begin not with the problem they want to solve, but with a related problem they can solve,
\begin{displaymath}{ } \mbox{ minimize } c^Tx \mbox{ subject to } Ax \leq b \end{displaymath} (0.2)

with some suitably chosen system $Ax \leq b$ of linear inequalities satisfied by all $x$ in ${\cal S}$: solving linear programming problems such as (0.2) is precisely what the simplex method is for.

Since (0.2) is a relaxation of (0.1) in the sense that every feasible solution of (0.1) is a feasible solution of (0.2), the optimal value of (0.2) provides a lower bound on the optimal value of (0.1). The ground-breaking idea of Dantzig, Fulkerson, and Johnson was that solving (0.2) can help with solving (0.1) in a far more substantial way than just by providing a lower bound: having satisfied oneself that the wallet is not under the streetlamp, one can pick the streetlamp up and bring it a little closer to the place where the wallet was lost. It is a characteristic feature of the simplex method that the optimal solution $x^{\ast}$ it finds is an extreme point of the polyhedron defined by $Ax \leq b$; in particular, if $x^{\ast}$ is not one of the points in ${\cal S}$ then it lies outside the convex hull of ${\cal S}$. In that case, $x^{\ast}$ can be separated from ${\cal S}$ by a hyperplane: some linear inequality is satisfied by all the points in ${\cal S}$ and violated by $x^{\ast}$. Such an inequality is called a cutting plane or simply a cut. Having found a cut, one can add it to the system $Ax \leq b$, solve the resulting tighter relaxation by the simplex method, and iterate this process until a relaxation (0.2) with an optimal solution in ${\cal S}$ is found.

We shall illustrate the Dantzig-Fulkerson-Johnson method on the Dantzig-Fulkerson-Johnson example, the 49-city problem. This instance of the TSP was created by picking one city from each of the 48 states of the U.S.A. (Alaska and Hawaii became states only in 1959) and adding Washington, D.C.; the costs of travel between different cities were defined as road distances taken from an atlas. (In the actual computations, each distance of $d$ miles was replaced by $(d-11)/17$ rounded up to the nearest integer, so that each of the resulting numbers could be stored as a single byte.) Rather than solving this 49-city problem, Dantzig, Fulkerson and Johnson solved the 42-city problem obtained by removing Baltimore, Wilmington, Philadelphia, Newark, New York, Hartford, and Providence. As it turned out, an optimal tour of the 42 cities used the edge from Washington, D.C. to Boston; since the shortest route between these two cities passes through the seven removed cities, this solution of the 42-city problem yields a solution of the 49-city problem.

Here, and throughout the paper, we shall conform to the following conventions. The symbol $V$ is reserved for the set of cities; each edge of the complete graph with vertex-set $V$ is simply a two-point subset of $V$; if $x$ is a vector whose components are indexed by the edges of this complete graph, then $x_e$ or $x(e)$ denotes the component indexed by $e$; we write

\begin{displaymath} x(S)= \sum (x_e: e\subseteq S)\hspace{0.73in} \end{displaymath}

for every set $S$ of cities and

\begin{displaymath} x(S,T)= \sum (x_e: e \cap S \neq \emptyset ,\; e \cap T \neq \emptyset ) \end{displaymath}

for every choice of disjoint sets $S,T$ of cities. By the graph of $x$, we shall mean the graph whose vertex-set is $V$, and whose edges are all the $e$ with $x_e>0$.

Trivially, each $x$ in ${\cal S}$ satisfies

\begin{displaymath}{ } 0 \leq x_e \leq 1 \mbox{\hspace{.45in} for all edges $e$} \hspace{1.15in} \end{displaymath} (0.3)

and
\begin{displaymath}{ } x(\{v\},V-\{v\})=2 \mbox{\hspace{.45in} for all cities $v$,} \hspace{1.55in} \end{displaymath} (0.4)

and so one can always use the system (0.3), (0.4) as the initial choice of the $Ax \leq b$ in (0.2).

In the 42-city problem, the graph of the optimal solution $x^{\ast}$ of this initial relaxation is disconnected: one of its two components has vertices 1,2,41,42 and the other component has vertices 3,4,...,40. This structural fault makes the first cut obvious: since every tour must cross every demarcation line separating $V$ into two nonempty parts at least twice, every $x$ in ${\cal S}$ satisfies

\begin{displaymath}{ } x(S,V-S) \geq 2 \end{displaymath} (0.5)

for all nonempty proper subsets $S$ of $V$; however, $x^{\ast}$ in place of $x$ violates (0.5) with $S=\{1,2,41,42\}$. Constraints (0.5), called ``loop conditions'' by Dantzig, Fulkerson, and Johnson, are nowadays called subtour elimination constraints or simply subtour constraints: from the set of integer solutions of (0.3), (0.4), they eliminate incidence vectors of disconnected graphs (consisting of two or more vertex-disjoint ``subtours'') and leave only the incidence vectors of tours.

The next two iterations are similar: the graphs of $x^{\ast}$ are disconnected and we add two more subtour constraints (one with $S=\{3,4,\ldots ,9\}$, the other with $S=\{24,25,26,27\}$). Then the graph of $x^{\ast}$ becomes connected but not 2-connected: removal of city 18 splits it into two connected components, one with vertices 13,14,...,17 and the other with vertices 19,20,...,42,1,2,...,12. Again, this structural fault in the graph points out a violated subtour constraint: more generally, if the removal of a single city, say $w$, splits the rest of the graph into connected components with vertex-sets $S_1,S_2,\ldots ,S_k$ ($k \geq 2$) then trivially $x^{\ast}(S_i,V-S_i)=x^{\ast}(S_i,\{w\}) \leq 1$ for at least one $i$. We add the subtour constraint with $S=\{13,14,\ldots ,17\}$ and continue through three similar iterations (adding subtour constraints with $S=\{10,11,12\}$, $S=\{11,12,\ldots ,23\}$, and $S=\{13,14,\ldots ,23\}$) until we obtain a relaxation (0.2), whose optimal solution $x^{\ast}$ is shown in Fig. 1.1: the solid edges $e$ carry $x_e=1$, the dashed edges $e$ carry $x_e=1/2$, and the long path 28-29-30- ...-41-42-1-2- ...-8-9-10 consists entirely of solid edges. The graph of this $x^{\ast}$ is 2-connected; no violated subtour constraints are apparent; in fact there are none.

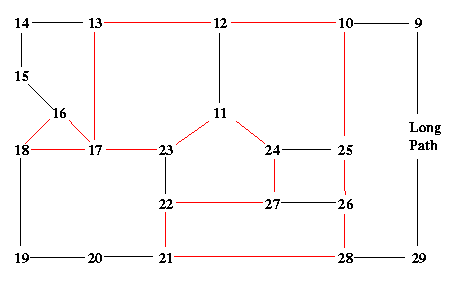
LP Solution

Fig.1.1: What is wrong with this vector?



Now Dantzig, Fulkerson, and Johnson add two more linear inequalities satisfied by all $x$ in ${\cal S}$ and say in a footnote, ``We are indebted to I. Glicksberg of Rand for pointing out relations of this kind to us''. These two inequalities read

\begin{displaymath}{ } x(\{15,16,18,19\})+2x_{\{14,15\}}+x_{\{16,17\}}+x_{\{19,20\}}\leq 6 \end{displaymath} (0.6)

(actually, this constraint is presented in [2] as our (0.6) minus the sum of the three equations $x(\{v\},V-\{v\})=2$ with $v=15,16,19$) and
\begin{displaymath}{ } \sum a_ex_e \leq 42 \end{displaymath} (0.7)

with $a_{\{22,23\}}=2$ and $a_e=1$ for all other $e$ except that $a_e=0$ when (i) $e=\{25,26\}$, or (ii) $x^{\ast}_e=0$ and $\vert e \cap \{10,11,\ldots ,28\}\vert=1$, or (iii) $x^{\ast}_e=0$ and $\vert e \cap \{10,21,25,26,27,28\}\vert\geq 1$. It is easy to see that each $x$ in ${\cal S}$ satisfies (0.6); in fact, each $x$ in ${\cal S}$ satisfies
\begin{displaymath}{ } x(\{15,16,18,19\})+x_{\{14,15\}}+x_{\{16,17\}}+x_{\{19,20\}}\leq 5\, ; \end{displaymath} (0.8)

the sum of (0.8) and the trivial $x_{\{14,15\}}\leq 1$ is (0.6). To check that each $x$ in ${\cal S}$ satisfies (0.7), assume the contrary: the incidence vector of some tour $T$ violates (0.7). Obviously, $T$ has to use the edge $\{22,23\}$ and has to avoid all the edges $e$ with $a_e=0$. Since $\{9,10\}$ and $\{28,29\}$ are the only two edges $e$ with $a_e\neq 0$ and precisely one endpoint in $\{10,11,\ldots ,28\}$, they have to be used by $T$; since $\{10,25\}$ and $\{24,25\}$ are the only two edges $e$ with $a_e\neq 0$ and one endpoint equal to 25, they have to be used by $T$; since $\{26,27\}$ and $\{26,28\}$ are the only two edges $e$ with $a_e\neq 0$ and one endpoint equal to 26, they have to be used by $T$. Since $T$ uses $\{26,28\}$ and $\{28,29\}$, it must avoid $\{21,28\}$; since $\{20,21\}$ and $\{21,22\}$ are the only remaining edges $e$ with $a_e\neq 0$ and one endpoint equal to 21, they have to be used by $T$. Since $T$ uses $\{21,22\}$ and $\{22,23\}$, it must avoid $\{22,27\}$; since $\{24,27\}$ and $\{26,27\}$ are the only remaining edges $e$ with $a_e\neq 0$ and one endpoint equal to 27, they have to be used by $T$. But then $T$ contains a cycle on 1,2,...,10,25,24,27,26,28, 29,...,42, a contradiction.

By adding constraints (0.6) and (0.7) to the previous relaxation of (0.1), Dantzig, Fulkerson and Johnson finally put the streetlamp next to the wallet: they obtained a relaxation, whose optimal solution is the incidence vector of a tour (passing through the 42 cities in the order of their labels). And that was the end of the 49-city problem.

The influence of this work reached far beyond the narrow confines of the TSP.

On the one hand, the method can be used to attack any problem of the form (0.1), regardless of the particular choice of ${\cal S}$, as long as there is an efficient algorithm to recognize points of ${\cal S}$ (we have to know a good thing when we see it returned as an optimal solution of a relaxation (0.2)). Many problems in combinatorial optimization have this form: in the maximum clique problem, ${\cal S}$ consists of the incidence vectors of all cliques in the input graph $G$ (the components of these vectors are indexed by the vertices of $G$); in the maximum cut problem, ${\cal S}$ consists of the incidence vectors of all edge-cuts in the input graph $G$ (the components of these vectors are indexed by the edges of $G$); and so on. In each of these particular examples, the challenge is to come up with linear inequalities satisfied by all the points in ${\cal S}$ and violated by the optimal solution $x^{\ast}$ of the current relaxation (0.2). To meet this challenge, one often begins with common sense to establish some combinatorial property of ${\cal S}$ and only then (as we have seen in the 42-city example) one expresses this property in terms of linear inequalities. This line of attack led to the development of the flourishing field of polyhedral combinatorics.

Second, the method can be used to attack any integer linear programming problem. (To cast the TSP in this form, note that its ${\cal S}$ consists of all integer solutions of (0.3), (0.4), (0.5).) Again, the challenge is to come up with linear inequalities satisfied by all the integer feasible solutions of the current relaxation (0.2) and violated by its optimal solution $x^{\ast}$: can I. Glicksberg's ingenuity be replaced by an automatic procedure to generate cutting planes? Ralph Gomory [3], [4], [5] answered this challenge with breathtaking elegance by his design of cutting-plane algorithms.

In this way, the work of Dantzig, Fulkerson, and Johnson became the prototype of two different methodologies: polyhedral combinatorics in combinatorial optimization and cutting-plane algorithms in integer linear programming.

Further discussions of cutting-plane algorithms for the TSP can be found in Padberg and Grötschel [6] and Padberg and Rinaldi [7]

This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.42)