
Some examples of trees.
Next: An algorithm to find derivations in PC
We give a second proof of the important compactness result, Theorem 8.1
of LMCS, using the visual aid of trees.
As background to the proof of the compactness theorem we want
to introduce the reader to basic notions regarding
trees. A tree is essentially an upside-down simplified representation
of an ordinary tree, e.g.,

Some examples of trees.
The key ingredients of a tree are the nodes, indicated in the above figure by solid black circles, and the edges connecting them. The node at the top is called the root of the tree, and those connected by an edge are said to be adjacent. Every node which is not the root has exactly one adjacent node above it. A tree is binary if every node has at most two adjacent nodes below it. The above examples of trees are binary.
A branch in a binary tree is a
path starting at the root and proceeding
downward along the edges of the tree, and not stopping unless it comes
to a node with no adjacent nodes below it. We give two examples
below, the first being a finite branch in a finite binary tree, the second
is meant to indicate an infinite branch in an infinite binary tree.
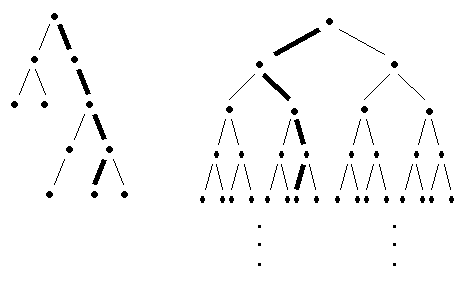
Branches in a tree
The length of a branch is the number of edges in the branch, which is one less than the number of nodes in the branch. A branch is infinite if it has an infinite number of nodes in it. A tree has arbitrarily long branches if for every positive integer n there is a branch in the tree with length at least n. Clearly a tree with an infinite branch has arbitrarily long branches. In the preceding figure we note that the first binary tree is finite and does not have arbitrarily long branches; whereas the second binary tree is infinite, has arbitrarily long branches, and has infinite branches. The following special case of a famous theorem, called König's Lemma, guarantees an infinite branch for certain binary trees.
Proof. The idea is simply that if there are arbitrarily long branches passing through a given node a of a binary tree, then for some node a' adjacent to a and immediately below it one must have arbitrarily long branches passing through a'.
To see this consider the two cases, namely we have one node a1 or two nodes a1, a2 adjacent to and below a. In the first case clearly all the branches through a go through a1, and we are finished. In the second case, if we have no branches of length ni going though ai, then there are no branches of length n = max(n1, n2) going through a. But this contradicts our assumption that there are arbitrarily long branches through a.
We can start with the root r and repeatedly apply this observation
to obtain an infinite branch ![]() .
.
Now we want to apply this lemma to show that a set of propositional formulas is satisfiable iff every finite subset is satisfiable. First we need a technical lemma.

Proof
The truth equivalence relation ![]() partitions
S into equivalence classes. Let S' be a subset
of S obtained by choosing exactly one member from
each such equivalence class.
Then S and S' are satisfied by precisely the same
truth evaluations for the variables of S.
partitions
S into equivalence classes. Let S' be a subset
of S obtained by choosing exactly one member from
each such equivalence class.
Then S and S' are satisfied by precisely the same
truth evaluations for the variables of S.
THEOREM [Compactness for Propositional Logic]
Let S be a set of propositional formulas.
Then Sat(S) iff
Sat(S0 )
for every finite ![]() .
.
Proof.
First we can use Lemma 2 to assume, without
loss of generality, that
no two formulas in S are truth equivalent.
The direction
( ![]() )
is clear, so let us prove
(
)
is clear, so let us prove
( ![]() ).
Let S be a set of propositional formulas such that each
finite subset of S is satisfiable.
).
Let S be a set of propositional formulas such that each
finite subset of S is satisfiable.
Let
![]() be the propositional variables occurring in
S; and let Sn be the set of formulas
in S which mention only variables from
be the propositional variables occurring in
S; and let Sn be the set of formulas
in S which mention only variables from
![]() .
Then
Sn
has at most
.
Then
Sn
has at most
![]() members (since different members have
different truth tables).
Thus if only finitely many variables occur in S
it follows that S is finite, and therefore satisfiable.
So now we assume infinitely many variables occur in S.
members (since different members have
different truth tables).
Thus if only finitely many variables occur in S
it follows that S is finite, and therefore satisfiable.
So now we assume infinitely many variables occur in S.
A truth evaluation is determined by an assignment of truth values
to the propositional variables. Now think of such an assignment
as a path through the following binary tree:
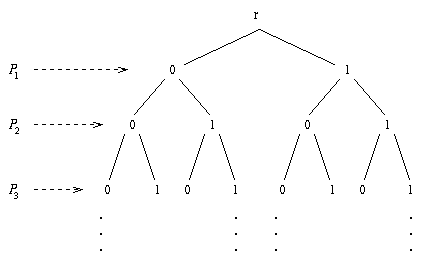
For example the assignment
![]()
will give the path
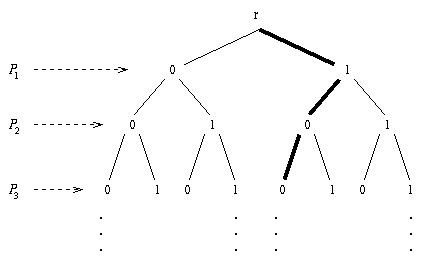
Let
TS
be the subtree of this binary tree given by taking all
the finite paths ![]() in the tree such that the
truth evaluation
in the tree such that the
truth evaluation ![]() makes every formula
in
makes every formula
in ![]() true. Then clearly
TS
is a binary tree, and since
one can satisfy any
true. Then clearly
TS
is a binary tree, and since
one can satisfy any ![]() , it must have arbitrarily long branches.
Thus, by Lemma 1, the tree
TS
must have an infinite
branch
, it must have arbitrarily long branches.
Thus, by Lemma 1, the tree
TS
must have an infinite
branch ![]() .
But then the truth evaluation
.
But then the truth evaluation
![]() makes all the formulas
in S true, i.e., S is satisfiable.
makes all the formulas
in S true, i.e., S is satisfiable.
Next: An algorithm to find derivations in PC
Stan Burris