1 - 6. Determine which of the following sentences are statements. What are the truth values of those that are statements?
- 7 > 5.
- 5 > 7.
- Is 5 > 7 ?
- 21/2 is an integer.
- Show that 21/2 is not an integer.
- If 5 is even then 6 = 7.
7 - 12. Write down the truth tables for each expression.
- NOT ( NOT P )
- NOT ( P OR Q )
- P => ( Q OR R )
- ( P AND Q ) => R
- ( P OR NOT Q ) => R
- NOT P => ( Q <=> R )
- P UNLESS Q is defined as ( NOT Q ) => P. Show that this statement has the same truth table as P OR Q. Give an example in common English showing the equivalence of P UNLESS Q and P OR Q.
- Write down the truth table for the exclusive or connective XOR.
- Write down the truth table for the not or connective NOR.
- Write down the truth table for the not and connective NAND.
17 - 21. Write each statement using P, Q, and connectives.
- P whenever Q.
- P is necessary for Q.
- P is sufficient for Q.
- P only if Q.
- P is necessary and sufficient for Q.
- Show that the statements P AND ( Q AND R ) and ( P AND Q ) AND R have the same truth tables. This is the associative law for AND.
- Show that the statements P AND ( Q OR R ) and ( P AND Q ) OR ( P AND R ) have the same truth tables. This is a distributive law.
- Is ( P AND Q ) => R equivalent to P => ( Q => R ) ? Give reasons.
25 - 28. Let P be the statement`It is snowing.' and let Q be the statement `It is freezing.' Write each statement using P, Q, and connectives.
- If it is snowing, then it is freezing.
- It is freezing when it is snowing.
- It is freezing but not snowing.
- When it is not freezing it is not snowing.
29 - 32. Let P be the statement `I can walk.' Q be the statement `I have broken my leg.' and R be the statement `I take the bus.' Express each statement as an English sentence.
- Q => NOT P
- P <=> NOT Q
- R => ( Q OR NOT P )
- R => ( Q <=> NOT P )
33 - 36. Express each statement as a logical expression using quantifiers. State the universe of discourse.
- There is a smallest positive integer.
- There is no smallest positive real number.
- There exists an integer that is larger than the product of any two integers.
- Every pair of integers has a common divisor.
37 - 40. Negate and simplify each expression.
-
 x ( P(x) OR Q(x) )
x ( P(x) OR Q(x) )
-
 x ( (P(x) AND Q(x) ) => R(x) )
x ( (P(x) AND Q(x) ) => R(x) )
-
 x ( P(x) => Q(x) )
x ( P(x) => Q(x) )
-
 x
x  y ( P(x) AND Q(y) )
y ( P(x) AND Q(y) )
41 - 44. If the universe of discourse is the real numbers, what does each statement mean in English? Are they true or false?
-
 x
x  y (x
y (x 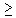 y).
y).
-
 x
x  y (x
y (x 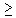 y).
y).
-
 y
y  x (x
x (x 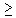 y).
y).
-
 x
x  y (x
y (x 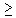 y).
y).
45 - 48. Determine whether each pair of statements is equivalent. Give reasons.
-
 x ( P(x) OR Q(x) ) (
x ( P(x) OR Q(x) ) ( x P(x) ) OR (
x P(x) ) OR ( x Q(x) )
x Q(x) )
-
 x ( P(x) AND Q(x) ) (
x ( P(x) AND Q(x) ) ( x P(x) ) AND (
x P(x) ) AND ( x Q(x) )
x Q(x) )
-
 x ( P(x) OR Q(x) ) (
x ( P(x) OR Q(x) ) ( x P(x) ) OR (
x P(x) ) OR ( x Q(x) )
x Q(x) )
-
 x ( P(x) OR Q(y) ) (
x ( P(x) OR Q(y) ) ( x P(x) ) OR Q(y)
x P(x) ) OR Q(y)
- If A, B and C are sets, the statement A
 B
B 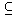 C can be expressed as
C can be expressed as
 x ( (x
x ( (x  A AND x
A AND x B ) => x
B ) => x C ) .
Express and simplify the negation of this expression, namely A
C ) .
Express and simplify the negation of this expression, namely A  B is not a subset of C, in terms of quantifiers.
B is not a subset of C, in terms of quantifiers.
- If A and B are sets, the statement A = B can be expressed as
 x ( x
x ( x  A <=> x
A <=> x B ) .
What does A not equals to B mean? Give different ways of expressing this using quantifiers. How would you go about showing that two sets are not the same?
B ) .
What does A not equals to B mean? Give different ways of expressing this using quantifiers. How would you go about showing that two sets are not the same?
- The definition of the limit of a function, limx -> a f(x) = L, can be expressed using quantifiers as

 > 0
> 0 
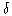 > 0
> 0  x ( 0 < | x - a | <
x ( 0 < | x - a | < 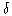 => | f(x) - L | <
=> | f(x) - L | <  ) .
Use quantifiers to express the negation of this statement, namely limx -> a f(x) is not equal to L.
) .
Use quantifiers to express the negation of this statement, namely limx -> a f(x) is not equal to L.
- Show that the statement P => ( Q OR R ) is equivalent to the statement ( P AND NOT Q ) => R .
[ This explains the proof method 0.3.6 for P => ( Q OR R ) . ]
- Show that the statement P => (Q AND R) is equivalent to the statement (P => Q) AND (P => R) .
[ This explains the proof method 0.3.7 for P => ( Q AND R ) . ]
- Is the statement P => ( Q => R ) equivalent to ( P => Q ) => R ? Give reasons.
- Show that the statement P AND Q AND R is equivalent to the statement ( NOT P AND NOT Q) => R) .
56 - 60. Negate and simplify each expression.
- If I do my assignments then I will get a good mark in the course.
- If x > 3 then x2 > 9.
- If x < -3 then x2 > 9.
- If a number is divisible by 2 then it is not prime.
- If x
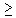 0 and y
0 and y 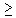 0 then x y
0 then x y 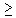 0.
0.
- Let a and b be real numbers. Prove that if a b = 0 then a = 0 or b = 0.
- Let A and B be sets. Prove that if x is not in A
 B then x is not in A or x is not in B.
B then x is not in A or x is not in B.
 x ( P(x) OR Q(x) )
x ( P(x) OR Q(x) )
 x ( (P(x) AND Q(x) ) => R(x) )
x ( (P(x) AND Q(x) ) => R(x) )
 x ( P(x) => Q(x) )
x ( P(x) => Q(x) )
 x
x  y ( P(x) AND Q(y) )
y ( P(x) AND Q(y) )
 x
x  y (x
y (x 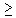 y).
y).
 x
x  y (x
y (x 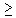 y).
y).
 y
y  x (x
x (x 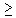 y).
y).
 x
x  y (x
y (x 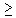 y).
y).
 x ( P(x) OR Q(x) ) (
x ( P(x) OR Q(x) ) ( x P(x) ) OR (
x P(x) ) OR ( x Q(x) )
x Q(x) )
 x ( P(x) AND Q(x) ) (
x ( P(x) AND Q(x) ) ( x P(x) ) AND (
x P(x) ) AND ( x Q(x) )
x Q(x) )
 x ( P(x) OR Q(x) ) (
x ( P(x) OR Q(x) ) ( x P(x) ) OR (
x P(x) ) OR ( x Q(x) )
x Q(x) )
 x ( P(x) OR Q(y) ) (
x ( P(x) OR Q(y) ) ( x P(x) ) OR Q(y)
x P(x) ) OR Q(y)
 B
B 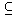 C can be expressed as
C can be expressed as
 x ( (x
x ( (x  A AND x
A AND x B ) => x
B ) => x C ) .
C ) .
 B is not a subset of C, in terms of quantifiers.
B is not a subset of C, in terms of quantifiers.
 x ( x
x ( x  A <=> x
A <=> x B ) .
B ) .

 > 0
> 0 
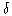 > 0
> 0  x ( 0 < | x - a | <
x ( 0 < | x - a | < 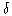 => | f(x) - L | <
=> | f(x) - L | <  ) .
) .
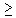 0 and y
0 and y 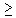 0 then x y
0 then x y 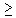 0.
0.
 B then x is not in A or x is not in B.
B then x is not in A or x is not in B.