The Algebra of Logic: Schröder

The monument to the work initiated by Boole, the algebraization of logic, is the three volumes Algebra der Logik by Schröder (1841-1902), which appeared in the years 1890-1910, filling over 2,000 pages. Although the spirit of the subject came from the work of Boole and De Morgan, Schröder's volumes are really a tribute to the work of C.S. Peirce, along with Schröder's contributions. In addition to the substantial job of organizing the literature, the lasting contributions of Schröder's volumes are 1) his emphasis on the Elimination Problem and 2) his fine presentation of the Calculus of Binary Relations.

Volumes I and II are devoted to the Calculus of Classes, with the standard operations of union, intersection and complement, adhering to Boole's arithmetic notation for union (+) and intersection ( ). Schröder was very much influenced by Peirce's work, and followed him in making the relation of subclass ( ) the primitive notion, whose properties are given axiomatically (what we now call the axioms for a bounded lattice, presented as a partially ordered set), then defining the other operations and equality from it.

One of the historically interesting items in Vol. I is Schröder's discovery that the distributive law does not follow from the assumptions Peirce put on . Schröder's proof is via a model, and indeed a rather complicated one (based on 990 quasigroup equations). Subsequently Dedekind published his first paper on dualgroups (= lattices) in 1897, giving a much shorter proof using a five element example (to show that a lattice need not be distributive).

The main goal of Schröder's work is stated most clearly in Vol. III, p. 241, where he says that

getting a handle on the consequences of any premisses, or at least the fastest methods for obtaining these consequences, seems to me to be the noblest, if not the ultimate goal of mathematics and logic.

Schröder is very fond of examples and is only too aware that one can get into computational difficulties with the Calculus of Classes. The examples worked out at the end of Vol. I show how demanding the methods of Jevons and Venn become as the number of variables increases. Such difficulties evidently led him to focus on Elimination. In deriving a conclusion from some hypotheses about classes it is often the case that some of the classes in the hypotheses do not appear in the conclusion. If one could find a such that

then one could concentrate on the apparently simpler problem of deriving from . Finding , the Elimination Problem, is the recurring theme of Schröder's three volumes.

At the end of his work on this problem for the Calculus of Classes he observed that in some cases of elimination he needed to refer to the number of elements in certain classes, a direction that did not appeal to him. However it was a direction that would later be used by Skolem with success (in the general case considered by Schröder). Indeed, Schröder avoided as much as possible the reference to elements in his formal development of the Calculus of Classes. He had no symbol for membership -- that would be first introduced by Peano. When Schröder finally does introduce elements of the domain into his formalism, he uses what we would call singletons, but identifies them with the elements. And he introduces them (Vol. II, §47) not as a primitive concept, but as a defined notion, his definition being equivalent to saying i is an element iff

A convention which can make reading the work of Schröder a bit slow today is his deliberate identification of the notation for the Calculus of Classes and for the Propositional Calculus -- an idea clearly due to Peirce. For example he will write (Vol II, p. 10) where we would write , where F denotes some canonical false statement. Thus = can mean , and can mean . The quantifiers and are introduced, following Peirce, and are used also in the Calculus of Classes for and .

Vol. III of Schröder is devoted to the Calculus of Binary Relations, pioneered by De Morgan, and largely developed by Peirce. In the Calculus of Classes one works with the subclasses of a domain D, whereas one works with the subclasses of D D in the Calculus of Binary Relations. One still has the operations , , ', and the constants 0, 1 as in the Calculus of Classes, but there are the additional operations of converse , relational product , and relational sum , as well as a constants for the diagonal relation and its complement. On p. 16 of Vol. III he discusses relations of n arguments, and says that statements involving such can be rephrased as statements involving binary relations, although the price may be the loss of transparency of meaning.

In contrast to his approach to the Calculus of Classes, Schröder develops the Calculus of Binary Relations making extensive use of the primitive notion of membership (again, following the development of Peirce). Schröder had no symbol for membership ( ), as we said above -- to say he would write . He says that the Calculus of Binary Relations is determined by 29 properties (Vol. III, §3), which we give in our language, but we retain his numbering:

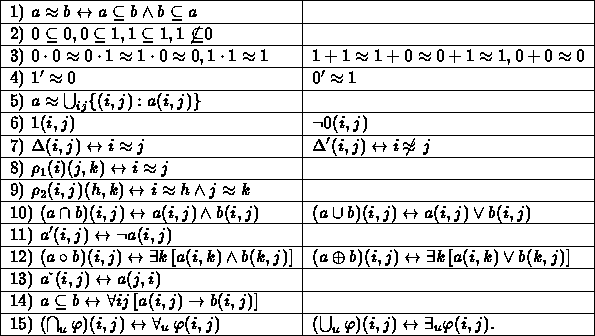
The Calculus of Binary Relations is incredibly more complex than that of classes. A considerable portion of this volume deals with the terms t(x) in a single unknown -- he is able to find 256 distinct ones before abandoning the problem. There are actually infinitely many distinct terms in one variable. Schröder also incorporated into his study of binary relations Pierce's notation for union and intersection, and , ranging over all the binary relations, notation which, as before, could also be used for quantifiers.

Thanks to the fact that is a term which takes the value 0 if x is 0, and 1 otherwise (Vol. III, p. 147), Schröder can reduce any finite set of atomic and negated atomic formulas to a single equation , provided the domain has at least two elements (which he always requires). For the case of a single variable, , he shows (Vol. III, p. 165) the general solution can be expressed by the following, given a particular solution a:

Unfortunately, as Schröder notes, this is not very useful, for if this gives , and otherwise it gives .

He also introduced toward the end of the third volume the use of and over the elements of the domain, but in a roundabout way. Namely he would identify an individual i of the domain D with the binary relation , which we have called in item 8), and then let and range over such relations. Such individuals are determined by the equation (Vol. III, p. 408). Relations which are singletons , which we called in item 9) are determined by the equation (Vol. III, p. 427). Also he embedded the study of classes into the study of binary relations by identifying a class A with . Relations associated with classes are then determined by (Vol. III, p. 450).

One of the few applications of the Calculus of Binary Relations given by Schröder to other areas of mathematics is the formulation and proof of a slight generalization of Dedekind the induction theorem (for chains). Also there is a formulation of Cantor's basic ideas on infinite classes. For example (Vol. III, p. 587) a binary relation x is a one-to-one correspondence iff it satisfies , a function iff it satisfies .

In Vol. III, p. 278, we see Schröder posing the question as to whether the algebra of binary relations will really provide the foundation for mathematics:

An important but difficult question is that of the of our algebra of binary relations, in particular the question of whether this discipline with its six operations suffices for all purposes of the pure and applied theories (in particular, for the logic of binary relations).

(By 1915 Löwenheim will have no doubts about the expressive power of binary relations.)

One of his claims towards the end of Vol. III, p. 551, involved what could be interpreted as a general method for passage from an expression involving quantifiers over individuals to one which does not. The possibility of expressing first-order formulas in the language of binary relations with equality as equations in the Calculus of Binary Relations, without resort to the use of above, would be picked up by Korselt, who showed that the statement ``there exists four distinct elements'' could not be so expressed. Löwenheim would turn to an examination of models of first-order statements in relational logic with equality, using the notation of Schröder, and this focused attention in mathematical logic on what we now call model theory.

The Calculus of Binary Relations is not nearly so widely known as the Calculus of Classes. It forms a substantial part of Vol. I of Principia Mathematica, and it has been a source of fundamental research under the name of Relation Algebras in the school led by Tarski. In 1964 Monk proved that, unlike the Calculus of Classes, there is no finite equational basis for the Calculus of Binary Relations. The recent book A Formalization of Set Theory without Variables (1988) by Tarski and Givant shows that relation algebras are so expressive that one can carry out first-order set theory in their equational logic.

One last note: Schröder's name is best known in connection with the famous Schröder-Bernstein theorem. Actually, the proof that Schröder gave in 1896 was full of holes (according to Fraenkel), and it was Bernstein, a student of Cantor, who produced a correct proof the next year.

References

1

E. Schröder, Algebra der Logik, I-III. 1890-1910. Chelsea reprint 1966.