
Using this we have expressed the lengthy argument of Lewis Carroll in the propositional calculus since all the statements are universal in Example 2.7.11 of LMCS.
Next: Comments on the nature of Boolean algebra
The universal Aristotelian statements can be expressed by
propositional formulas as follows:

Using this we have expressed the lengthy argument of
Lewis Carroll in the propositional calculus
since all the statements are universal in Example 2.7.11
of LMCS.
Unfortunately we do not have a translation of I,O statements into propositional formulas.
The simplest ``upgrade'' of the propositional calculus which is adequate
to handle the I,O statements is the monadic predicate calculus
which deals with quantified first-order statements about unary predicates.

We can translate propositional logic into the Calculus of
Classes by letting
![]() be the conversion of propositional formulas into
Calculus of Classes terms obtained by simply replacing
be the conversion of propositional formulas into
Calculus of Classes terms obtained by simply replacing
![]() with
with
![]() ,
,
![]() with
with
![]() , and
, and
![]() with '; and then
observing that an argument
with '; and then
observing that an argument
![]()
is valid in the Propositional Logic iff
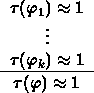
is valid in the Calculus of Classes.
Conversely, given an equational argument in the Calculus of Classes we
can assume that it is in the form
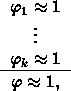
and reversing our translation we have a corresponding argument in the propositional logic.
In summary we have a translation of arguments in the propositional calculus into arguments in equations in the calculus of classes, and conversely.
Hence they can be thought of as equivalent.
Both are adequate to handle the universal Aristotelian statements.
To strengthen the Calculus of Classes to handle I and O statements we
only need to add
![]() . No such easy strengthening is available for
the propositional logic.
. No such easy strengthening is available for
the propositional logic.
Next: Comments on the nature of Boolean algebra
Fri Jan 31 11:14:47 EST 1997