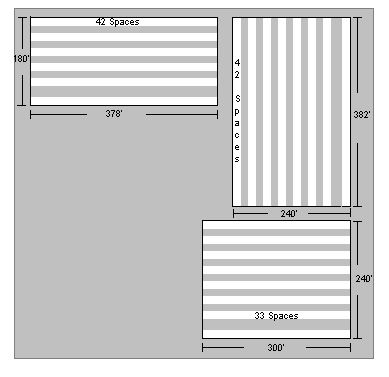
The purpose of this project is to develop a model for determining an optimum parking layout of a given rectangular paved lot. The objective of this problem is to either maximize the number of parking spaces or the area of each parking space in the giv en lot, subjected to a number of regulations and constraints. In particular, each parking space is 9 feet by 18 feet and the access lanes are 12 feet wide. The problem also asked that we optimize the layout of the University of Waterloo, Parking Lot B. The dimensions of this lot can be found in Appendix A.
The choice of the constraints should be made carefully so that the model can be applied to any real situation. There are many constraints that are considered in solving the problem. Some examples of the constraints are the dimension of each parking s pace, the width of the access lane, the layout of a parking space, and the location of the entrance of the lot.
Due to the integral nature of the model, it is very difficult to perform the usual sensitivity analysis such as cost ranging. The following analysis is conducted to estimate the change in the objective value by changing one parameter of parking lot B3 .
When the width is increased by 10 to 310, the change in optimal parking spaces is (272 264) = 8. The approximate shadow price is thus 0.8.
When the width is increased by 100 to 400, the change in optimal parking spaces is (352-264)=88. The approximate shadow price is thus 0.88.
It appears that an increase in the parking lot width increases the number of parking spaces in a stepwise manner. The orientation of the parking spaces has not changed.
When the length is increased by 1 to 241, there is no change in the number of optimal parking spaces. The approximate shadow price is thus 0.
When the length is increased by 2 to 242, there is no change in the number of optimal parking spaces. The approximate shadow price is thus 0.
When the width is increased by 3 to 243, the orientation of the parking spaces changed from a horizontal placement to a vertical placement.
The number of parking spaces increased by 6. This means we have found an upper bound for the parking lot length, specifically, Length < 243.
When the width is increased by 1 to 10, the change in optimal parking spaces is (240-264)= -24. The approximate shadow price is thus 24.
When the width is increased by 2 to 11, the change in optimal parking spaces is (216-264)= -48. The approximate shadow price is thus 24.
It appears that the shadow price is 24 and it does not seem to behave in the stepwise manner as seen in part 1).
When the length is increased by 1 to 31, the orientation of the parking spaces changed from a horizontal placement to a vertical placement. The number of parking spaces increased by 3. This means we have found an upper bound for the parking space l ength, specifically, Plength < 31.
When the width is increased by 10 to 310, the change in optimal parking spaces is (310-300) = 10. The approximate shadow price is thus 1.
When the width is increased by 30 to 330, the change in optimal parking spaces is (330-300) = 30. The approximate shadow price is thus 1.
It appears that the shadow price is 1 and it does not seem to behave in the stepwise manner.
When the length is increased by 5 to 245, there is no change in the number of optimal parking spaces. The approximate shadow price is thus 0.
When the length is increased by 10 to 250, there is no change in the number of optimal parking spaces. The approximate shadow price is thus 0.
The upper bound on this parameter is not computed due to technological constraints.
The nature of this model prohibits the sensitivity analysis such as cost ranging and right hand side ranging. This is because the parking lot dimensions are specified in the sets instead of as a constraint. The change in parking lot sizes will change the number of variables involved in the problem.
The change in the parking lot sizes will change the placement and orientation of the parking spaces, which is basically the diagram of how things are located.
Due to technical and feasibility constraints (CPU time, Iteration Limits, Run time), it is impossible to even run the model for an actual parking lot. Hence, it is not feasible to perform perturbations of parking lot dimensions.
The models provided below will optimize the number of parking spaces in a rectangular parking lot. Since Parking Lot B at the University of Waterloo is actually comprised of three rectangular parking lots, the optimal solutions are obtained by optimiz ing each of the three lots.
The most basic model involves only two options: arranging parking spaces horizontally or vertically. (Straight parking spaces refer to the situation when the parking space is at a 90o angle to the access lane.) Note that the parking space length include 12 of access lane space. The model is thus defined as follows:
Width : The width of the parking lot / n /
Length : The length of the parking lot / m /
Pwidth : The width of a parking space / 9 /
Plength : The length of a parking space / 18 /
The number of parking spaces if they are placed vertically.
The number of parking spaces if they are placed horizontally.
The optimal number of parking spaces
Maximize Z = MAX( X, Y )
The objective function
Subject To X = trunc(Length / Pwidth) * trunc(Width / Plength)
This model made the following assumptions:
The model is very simplistic due to the number of assumptions that are made. Some of the assumptions are not likely to occur in the real world. Another criticism is that this model is solved in GAMS using DNLP (Discrete Non-Linear Programming) instea d of LP or MIP. However, since there are only two variables and two constraints involved, GAMS can solve the problem efficiently, even though it involves the use of a non-linear programming method.
The following extensions will attempt to incorporate some of the above assumptions into the model.
Diagonal parking spaces are only useful in some circumstances. In order to modify the above model to accommodate diagonal parking rows, it is first necessary to determine the length and width of each row, as well as the space "wasted" at the beginning and end of each row. Note also that the access lanes can be less than 12 feet in a one-way setting since cars do not have to turn the full 90o angle. Assume the parking space is at a 45 o angle, the access lane could be decreased by 1 on a one way lane, the length of the parking space is: Length = 18 * Cos(45 o) = 12.73 So, PDlength = 12.73 + 11 = 23.73 and Waste = 2 * 18 * Sin(45 o) = 25.46 The width of the parking space is the same.
The model is defined as below:
Length : The length of the parking lot / m /
Width : The width of the parking lot / n /
PSlength : The length of a straight parking space / 30 /
PSwidth : The width of a straight parking space / 9 /
PDlength : The length of a diagonal parking space / 23.73 /
PDwidth : The width of a diagonal parking space / 9 /
Waste : The unusable space from diagonal parking / 25.46 /
The number of straight parking spaces if they are placed vertically
The number of straight parking spaces if they are placed horizontally
The number of diagonal parking spaces if they are placed vertically
The number of diagonal parking spaces if they are placed horizontally
The total number of parking spaces
Maximize Z = MAX ( X,Y, P, Q )
The objective function subject to
X = trunc(Length / PSwidth) * trunc(Width / PSlength)
Y = trunc(Length / PSlength) * trunc(Width / PSwidth)
P = trunc( (Length Waste) / PDwidth ) * trunc(Width/PDlength)
Q = trunc(Length / PDlength) * trunc( (Width Waste) /PDlength)
X, Y, P, Q positive
This model made the following assumptions:
This model relies on a lot of simplifying assumptions. Although it is slightly more complicated than the Basic Model, it contains only four constraints and four variables, so it is still very efficient to solve with GAMS (even with non-linear programm ing). The model may not provide the optimal solution however, since the orientation of each parking space must be the same. Also, there could be other considerations such as whether the angle to the access lane is actually feasible for a car to enter. As well, the use of the 45 o in the model is arbitrary, and may not be the best angle to arrange the parking spaces.
The binary parking lot model is a different way of approaching the parking lot optimization problem. This model will only take into account "straight" parking spaces. With this model, there is some liberty in the orientation of the parking spaces, namely, it can either be vertical or horizontal. Given that the parking spaces should be 9 by 18 and the access lanes should be 12 wide, it is suggested to divide the parking lot into 3 by 3 squares, with each parking space occupying 18 squares. However, the problem could become really large as th e parking lot size increases, and given that it is a binary model, it is unlikely that any program could solve the problem efficiently. Hence, the model is scaled down with the parking lot divided into 9 by 9 squares. Also, for simplicity, the access lanes are assumed to be 9 in this model. (Note, each parking space occupies 2 squares, and an access lane portion occupies 1 square.) Let p = trunc( n/9 ) and q = trunc( m/9 )
I : The set of 9 by 9 squares along the parking lot width / 1 * p /
J : The set of 9 by 9 squares along the parking lot length / 1 * q /
Entrance : The least number of entrances to the access lane
P(I,J) : An indicator variable for the parking space, 1 for parking space, 0 for access lanes/unused areas
Int : An all-purpose integer variable
Z : The total number of squares used
Maximize Z = SUM((I,J), P(I,J))
# The objective function
Subject To SUM(J, 1-P(1,J)) + SUM(I, 1-P(I,1)) +
SUM(J, 1-P(p,J)) + SUM(I, 1-P(I,q))= Entrance
# Provides at least one opening to the parking lot
P(I,J) = P(I+1,J) + P(I,J+1) + P(I-1,J) + P(I,J-1)
2 + 2*P(I,J) = P(I+1,J) + P(I,J+1) + P(I-1,J) + P(I,J-1)
# These constraints restrict the orientation of the parking spots and the continuity of access lanes.
P(I,J) + P(I+1,J) <= 3 P(I+2,J) P(I-1,J)
P(I,J) + P(I,J+1) <= 3 P(I,J+2) P(I,J-1)
P(I,J) + P(I-1,J) <= 3 P(I-2,J) P(I+1, J)
P(I,J) + P(I,J-1) <= 3 P(I,J-2) P(I,J+1)
# These constraints restricts the position and number of openings given a parking space orientation.
SUM((I,J), P(I,J)) / 2 Int = 0
# This constraint will ensure an even number of parking squares are used.
P : Binary Int and I : Integer
The model allows for parking spaces to have different orientations to optimize the use of the parking lot. It also ensures that each parking space is attached to an access lane. An advantage is that the model concept is simple to understand. However , this program requires a large number of variables, and thus will be inefficient to execute, especially when the model involves integer variables. Also, program like GAMS may interpret the constraints strangely for the items outside of the set definitio n (e.g. I-1 could be 0, and GAMS may treat the variable strangely). Hence, it may be necessary to define additional constraints that takes care of the marginal values of the sets (i.e., 1, p, and q). This could be a hassle and leads to errors if the par king lot size is changed since the additional constraints must be changed as well.
The lamp posts restricts the location of the edge of the parking spaces since we cannot have a lamp post in the middle of a parking space. The approach to solve this problem is to divide the problem in such a way that each lamppost is on the edge of t he "new" parking lot. This is simple since we are merely solving many smaller problems with the above model.
Since a new model is not required, there is no need to critique the model in this section.
This model incorporates handicapped parking spaces into the calculation for the optimal layout.
I : the type of parking spaces / 1, 2 /
J : the options in finding number of areas of type 1 parking space / 1,2 /
A(I) : the area of parking spaces
Tpark : the total area of the given parking lot
Pwidth : the parking lot width
Plength : the parking lot length
W1 : the parking space width of type 1
L1 : the parking space length of type 1
X(I) : the number of parking spaces used
Y(J) : the wasted area from options for finding maximum number of areas of type 1 parking space
M : the minimum wastes from the first row option
U : the total parking lot area minus first row of parking space
Z : the total number of parking spaces used
Maximize Z=SUM(I, X(I))
# This is the objective function which maximizes the parking area
Subject To Y(1) = Pwidth*L1)-(trunc(Pwidth/W1))*W1*L1
# This finds the left over area when we layout the parking space vertically in the width of the parking lot
Y(2) = Plength*L1)-(truncPlength/W1))*W1*L1
# This finds the left over area when we layout the parking space vertically in the length of the parking lot
M = MIN(Y(1), Y(2))
# This finds the minimum of the left over areas so that the layout that gives the minimum left over area is used.
IF (M=Y(1), U.fx=TPark - Pwidth*L1
ELSE U.fx=TPark - Plength*L1
U=sum(I, A(I)*X(I))
# If the first layout using the width of the parking lot gives the minimum waste area then we subtract that first row of the parking spaces from the total area of the parking lot. The area found by this will be used to maximize the number of type 2
and 3 parking spaces. If the second layout using the length of the parking lot gives the minimum waste area then we subtract that first row of the parking spaces from the total area of the parking lot.
X(2)>=2
X(2)<=4
# This is to set a constraint on the handicap parking spaces. We assumed that there is two to four number of handicapped parking spaces.
X(I)>=0
# This is the nonnegative constraint
(parking lot length*length of the regular parking space ) - (max number of area of regular parking spaces that fits parking lot length*regular parking length )
and (parking lot width*length of the regular parking pace) - (max number of area of regular parking spaces that fits the area parking lot width*regular parking length)
The model maximizes the number of areas of parking spaces. We assumed that there are no handicap parking space for the first row of the parking lot to find the minimum waste area. This may not be the case in the real situation. Also, the handicap pa rking spaces are usually located side by side but this was not considered in the model.
This approach is taken from the UMAP journal of 1988. It involves using tiles and calculating for the optimal position for each tile. Each tile consists of a parking space, an access lane portion, and another parking space. To formulate this problem , it is first necessary to determine the possible place a tile could go. The paper uses twelve positions in formulating their model.
The program will start with a tile and then choose one position to place the other tiles until no more new tiles can be placed. The program will then try the other positions to arrive and compare to the previously computed solutions to arrive at the o ptimal placement. This means that the program will create a tree and the optimal solution is found by choosing the path that leads to the most parking spaces.
This approach is inefficient however, since the tree could grow exceptionally large. The team, which uses this method, restricts the problem by optimizing blocks of tiles instead of individual tiles. This problem does not allow for "turning corn ers", since the parking spaces and access lanes are formulated using tiles. Finally, this model made the assumption that parking spaces are "straight" when in fact it could be diagonal.
The parking lot problem could be formulated into a cutting stock problem. This involves dividing the parking lot into pieces of "raw" and determining the possible patterns that can be generated using that piece of raw. This approach will co nsider irregular sizes and shapes of parking lots when determining the optimal solution. There are some difficulties in formulating the cutting stock problem because vertical and horizontal parking spaces have the same area, and it is difficult to determ ine which type is used, if the stock is simply cut based on area. Hence, there is a need to consider the "raw" in two dimensions, that is other than optimizing area, there should be constraints on the length and width of the "raw". T here is also the difficulty of defining the best size of the raw, since having a raw too small restricts the type of parking spaces used, and defining the raw too large can cause redundant calculations.
Another approach that is related to the cutting stock problem is to formulate a two-dimensional knapsack problem. The parking spaces will be assigned a value of 1 and the access lane pieces, which are 1 by 1, will be assigned a value of 0. The weig ht will be defined in terms the parking spaces length and the width. The length and width of the parking lot serves as the supply constraint, such that each type of parking space can use no more than the supply. The knapsack problem will solve the opti mal number of each shape used. The shapes can then be organized back into a parking lot, which will have the optimal layout. A criticism of this approach is that it is solving two integer problems, which could be really inefficient. Also, the second pr oblem (placement of the given number of parking space types) may involve the use of a matrix. If the second problem is solved by GAMS, the model must be formulated as some sort of binary model and will e subjected to the same criticisms as the Binary Par king Lot Model.
The validity of this solution relies on GAMS ability to choose the placement that will result in the largest number of parking spaces. Since there are only two types of placements allowed and only one-way access lanes are used, this is equivalent to t rying to divide the parking lots into plots of 9 by (18+12)=30. This is exactly what the model attempts to calculate. Both orientations are calculated by two separate constraints and the model will choose the variable that has the most parking space s. The orientation of the spaces are easily deduced by looking at which of X and Y does the optimal value corresponds to. Hence, providing GAMS operate accurately, the solution given is valid.
The difference between this model and the previous one is the additional constraints and variables which calculates the number of diagonal parking spaces that can fit into the lot. Providing that the calculation of diagonal parking spaces in a row is
accurate, the solution is valid by reasons given in the previous section.
The diagonal parking spaces will result in unusable space at the end of each row. However, the access lane width will reduce since cars need less space to turn. Assuming that the parking spaces are at a 45o angle, the wasted space will be the
"triangle bits" at each end. We know that the length of the parking spaces have to be 18, so using trigonometry, we can calculate the waste at one end, which turns out to be 12.73 (See Model for calculation). Hence, the unusable space in ea
ch row is 2 x 12.73 = 25.46. Also, the length of the row will decrease, and using trigonometry again, we found that the row height is 12.73. We will assume that the access lane width can be decreased to 11. So, PDlength (row height + access lane wi
dth) is 23.73. Note that the PDwidth will remain at 9.
These dimensions are used in the model and hence if GAMS operate as expected, the solution given will be valid.
The validity of the solution again depends on the models validity and GAMS ability to operate correctly. The validity of the model is examined in the Models and Extensions section, and GAMS is assumed to operate correctly.
The model finds a non-integral optimal solution . It minimizes the unused portion of the parking lot for the parking layout. Because of non-integral optimal solution, the user must use only the integer part of the basic variable as the maximum number of parking spaces for each type of parking space. However, this rounded-down solution may be not be the optimal. Care must be given in interpreting the results.