The Riemann Sum Approximation to an Integral:

For a continuous function on a closed and bounded interval, the upper and lower Riemann sums converge, from above and below respectively, to some which we call the Riemann integral of the function as the step width goes to zero.

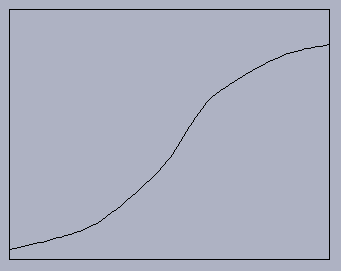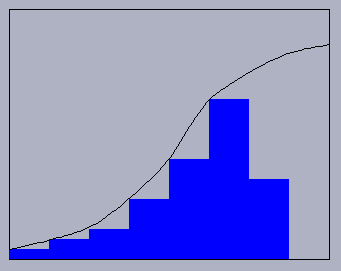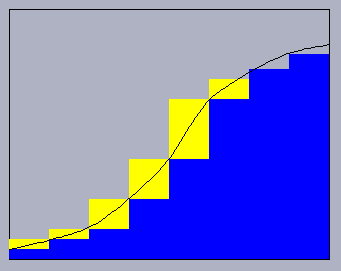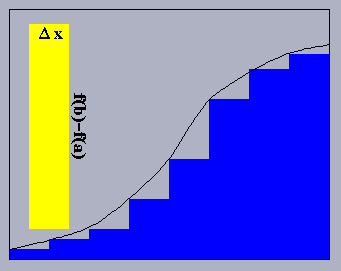
The animation above provides a convincing demonstration that this is indeed the case, at least for a monotone function. As the function f is increasing on the interval [a,b], the lower Riemann sum is obtained by evaluating the function at the left endpoint of each interval. The animation draws these in first. After that, the upper sum is drawn in. The difference in area between these two is collected together into a bar whose height is f(b)-f(a) and whose width is the step width delta-x. The area is the product of these two. As the width goes to zero, then so does the difference in area associated with the upper and lower sums.