저희는 한국의 모든 술집을 걸어서 방문하는 최단 거리를 구하는 문제를 풀었습니다.
외판원 문제 (TSP)로 알려진 이 문제를 한국에 있는 81,998개의 술집에 대하여 푼 것은 세계 최초입니다.
경찰청에서 제공하는 전체 술집 목록을 이용하고, 그 사이 이동하는 시간은
오픈 소스 라우팅 머신(OSRM)을 사용하여 술집 두 개의 쌍 3,361,795,003개 각각에 대하여 계산하였습니다.
우리가 찾은 경로는 OSRM 시간으로 측정했을 때 81,998개의 모든 술집을 방문하는 가장 짧은 경로라는 수학적 증명까지 된 경로입니다.
한국의 모든 술집을 방문하려면 최적의 경로로 방문한다고 하여도 매우 오래 걸립니다.
쉬지 않고 총 15,386,177초 즉 178일 1시간 56분 17초가 걸립니다.
물론 이 긴 길을 다니면서 마시다보면 딱 그 시간에 마치는 것은 거의 불가능하겠습니다. (완주하려면 술보다는 물이나 차 같은 건강에 좋은 것들을 마시는 것이 좋을 듯 합니다.)
그러니 초까지 세는 것이 무슨 의미가 있냐고 하실 수 있습니다.
하지만 우리가 계산하여 찾은 경로는 단순히 좋은 경로일 뿐만 아니라 81,998개 술집을 모두 방문하고 돌아오는 외판원 문제의 최적의 답입니다.
방문하는 순서를 조정하더라도 OSRM에서 추정한 도보 시간을 단 1초라도 절약할 수 없습니다.
이번에 계산해낸 한국의 모든 술집 방문 경로는 도로에서 경로를 찾는 TSP 문제 중에서 최적의 경로를 계산하는데 성공한 사례 중 가장 방문지점 수가 많습니다. 직전까지 최대 기록은 2021년 2월에 해결된 네덜란드의 57,912개 지점을 거치는 자전거 경로입니다.
이번 계산은 2024년 12월에서 2025년 3월 사이에 로스킬데 대학교와 워털루 대학교에서 하였습니다. 계산 작업에 대한 자세한 내용은 계산 페이지에서 확인할 수 있습니다.
경로 살펴보기
아래 그림은 korea81998 경로의 대화형 지도의 스크린샷입니다.
왼쪽의 메뉴에서는 7개 지역 중 하나를 선택하여 볼 수 있습니다.
오른쪽 상단에서 컬러 거리 지도 또는 거리 레이블이 없는 회색조 지도를 선택할 수 있습니다.
이 메뉴 바로 아래에서 정류장 마커를 표시할지, 경로 가장자리를 표시할지 또는 둘 다 표시할지 선택할 수 있습니다.
이미지를 클릭하면 지도를 볼 수 있습니다.
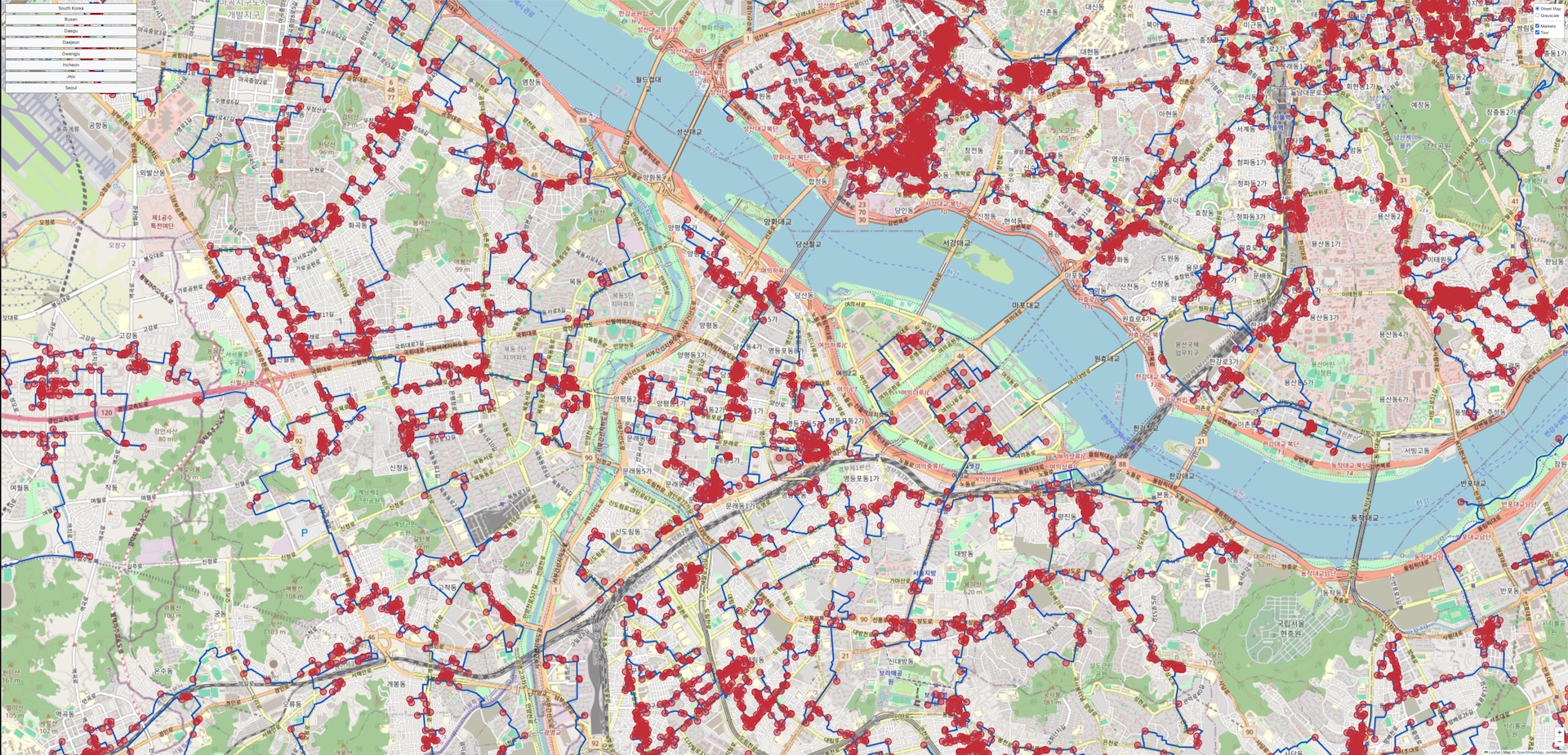
최적 경로의 일부 지역 모습
대화형 지도를 보는 데 문제가 있는 경우 아래 그림을 클릭하여 경로의 고해상도 이미지를 볼 수 있습니다.
도시 지역의 클로즈업 보기는 도시 페이지를 참조하세요.
최적화
요즘도 종종 현재의 컴퓨터로는 아주 작은 TSP 문제도 해결하는 것이 불가능하다는 이야기가
신문, 잡지, 블로그, 과학 기사 보도 자료에 나올 떄가 있습니다.
워싱턴 포스트에 실린 다음과 같은 전형적인 예가 있습니다.
"예를 들어, 노트북 컴퓨터로 22개 도시 간의 가장 효율적인 경로를 계산하려면 1,000년이 걸릴 것입니다."
이와 같은 기사는 TSP를 해결하는 유일한 방법이 가능한 경로를 하나씩 확인하는 것이라고 가정합니다.
물론 그런 식으로는 우리가 해결한 방문지점 수가 매우 많은 문제를 전혀 풀 수 없는 것은 맞습니다.
korea81998 사례의 경로 수는 대략 2 뒤에 0이 367308개입니다.
이렇게 많은 수의 경우를 모두 다 해본다는 것은 어마어마하게 어려워 보이지만, 이렇게 방문지점 수가 많은 TSP 문제를 해결할 수 없다는 것은 아닙니다.
저희는 매우 우수한 TSP 경로를 찾기 위한 LKH라는 프로그램과 최적임을 증명하기 위한 방법인 "절단 평면 방법"을 적용하기 위한 Concorde라는 프로그램을 잘 결합하여 문제를 풀 수 있었습니다.
이러한 도구를 적용하는 방법에 대한 간략한 설명은 계산 페이지에서 확인할 수 있습니다.
제가 예전에 쓴 짧은 글에서 절단 평면 방법을 간략히 설명한 내용이 있습니다 Scientific American
"아이디어는 요기 베라(Yogi Berra)의 조언을 따르는 것입니다. '길에서 갈림길에 다다르면, 그 길을 따라가세요.' 선형 계획법이라는 도구를 사용하면 바로 이 작업을 할 수 있습니다. 도로를 사용할지 말지 즉시 결정하지 않고 대신 도시 쌍을 연결하는 도로에 0과 1 사이의 유리수 값을 할당할 수 있습니다. 이 모델에서는 두 갈래의 길을 따라 외판원의 절반씩 보내는 것이 허용됩니다."
"이 과정은 모든 도시에 대해 그 도시로 들어오는 도로에 할당된 값의 합, 그 도시에서 나가는 도로에 할당된 값의 합이 각각 1이 되어야 한다는 제약으로 시작합니다. 그런 다음 단계별로 도로에 할당된 값들의 여러 가지 합에 관한 부등식으로 표현된 제약이 추가됩니다. 이렇게 반복하면 결국 선형 계획법을 통하여 각 도로에 대한 최적의 결정, 즉 가능한 가장 짧은 경로를 구할 수 있습니다."
몇 분만 시간이 있다면 국립 수학 박물관에서 영어로 진행한 최적의 투어에 대한 강연 영상을 시청해 보세요. 이 영상에서는 해당 방법이 자세히 설명되어 있습니다.
또는 한국 주제에 맞춰서 2024년 3월 KAIST에서 진행한 아마존 배송, 술집 산책, 우주 투어라는 제목의 강연 영상을 시청해 보세요.
P 대 NP
TSP와의 연결을 포함한 P 및 NP 복잡도 클래스에 대한 훌륭한 논의는 Lance Fortnow 교수가 쓴 글에서 찾을 수 있습니다. Fifty Years of P vs. NP and the Possibility of the Impossible.
 Credit: https://cacm.acm.org/research/fifty-years-of-p-vs-np-and-the-possibility-of-the-impossible/
Credit: https://cacm.acm.org/research/fifty-years-of-p-vs-np-and-the-possibility-of-the-impossible/
큰 그림
우리는 대규모 TSP 문제를 범용 최적화 방법을 개발하고 시험하기 위하여 사용합니다.
이 세상에 계산에 쓸 수 있는 자원이 무제한 있는 것이 아닙니다.
수학적 최적화와 운용 과학이라는 응용 수학 분야의 목표는 이러한 자원을 가능한 한 효율적으로 사용할 수 있도록 돕는 도구를 만드는 것입니다.
수학적 모델링이 산업, 상업, 의학 및 환경에 미치는 영향에 대한 일반적인 정보는 수학 연구와 교육을 지원하는 여러 학회를 통하여 얻을 수 있을 것입니다.
미국수학회 (American Mathematical Society),
미국 수학 협회 (Mathematical Association of America),
수학적 최적화 협회 (Mathematical Optimization Society),
INFORMS (운용 과학 분야),
미국산업응용수학회 (SIAM) (응용 수학 분야).
연구팀
William Cook, 캐나다 워털루 대학교, 조합론 및 최적화과
Daniel Espinoza, 칠레, Alicanto Labs
Marcos Goycoolea, 칠레 Adolfo Ibáñez 대학교, School of Business
Keld Helsgaun, 덴마크 로스킬레 대학교, Computer Science
감사의 말
계산에서 발생한 엄청난 수의 선형 계획법 모델은 IBM CPLEX Optimizer로 해결되었습니다.
IBM이 훌륭한 소프트웨어를 학술 연구에 무료로 제공해 주셔서 대단히 감사드립니다.
경로의 지도 그림은 대화형 지도를 위한 오픈소스 JavaScript 라이브러리인 Leaflet을 사용하여 만들어졌으며, OpenStreetMap, Carto Basemaps 및 Stadia Maps에서 만든 지도 타일을 활용했습니다.
기초과학연구원(IBS) 이산수학그룹의
엄상일 박사가 한국의 술집 위치를 경찰청이 관리하는 데이터베이스에서 다운로드하여 제공해 주었습니다.
지점 간 도보 시간 표는 오픈 소스 라우팅 머신 (OSRM)을 사용하여 만들어졌습니다.
기타 도로 여행
일본 편의점 40,426개.
영국에는 49,687개의 술집이 있습니다.
미국의 역사적 장소 49,603곳.
네덜란드 기념물 57,912개.
추가 자료
TSP의 역사, 응용 분야, 솔루션 기술 등을 소개하는 내용입니다.

TSP를 위한 절단면법에 대한 상세한 계산 연구.

P 대 NP 문제와 그 결과에 대한 간단한 소개입니다.

TSP를 사용하여 단 한 줄로 예쁜 이미지를 만드는 방법을 살펴보세요.

TSP 근사 알고리즘 이론에 관한 최신 연구.

TSP의 응용 프로그램은 1994년에 출판된 책에 실려 있으며, 현재 무료로 다운로드할 수 있습니다.