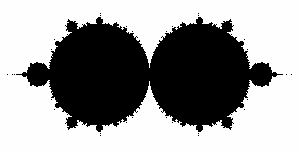 |
This is the section where
b = - a + 2
This is the view shown on Plate 189 of Mandelbrot's book, since the function
F ( z ) = ( 1 / a ) ( z + b + ( 1 / z ))
is conjugate to the function
b z ( 1 - z ) when a + b = 2.
The Mandelbrot set consists of the parameters ( a, b ), in 4-dimensional space, for which the filled-in Julia set is connected. We illustrate various 2-dimensional sections of this 4-dimensional set where
The function F( z ) has critical points at 1 and -1, and one of its three fixed points at infinity. Infinity is an attractive fixed point if and only if |a| < 1.
|
The standard Mandelbrot set
This is the section where b = - a + 2 This is the view shown on Plate 189 of Mandelbrot's book, since the function |
|
Snowshoe
This is the section where b = - a - 2 |
|
Spyglass
This is the a-plane section where b = ( - 1 + 0.4 i ) a + 2 |
|
Wink
This is the a-plane section where b = - a + 1.7 + 0.3 i |
|
Tie and Cane
This is the b-plane section where a = - b + 50 + 200 i |
|
Napoleon
This is the a-plane section where b = - a + 3 |
|
Sperm
This is the a-plane section where b = ( 0.3 - 0.4 i ) a + 1.2 + 0.3 i |
|
Ring
This is the b-plane section where a = ( 0.3 - 0.4 i ) b + 1.2 + 0.3 i |
|
Blood Clot
This is the a-plane section where b = 0 |
|
Alien
This is the (1/a)-plane section where b = 0 This is the same set as the previous image, but with a different form of the parameter. |
|
Scallops
This is the (1/a)-plane section where b = 2 |