Inversive Circles

in the Fractal Gallery of William Gilbert

Pure Mathematics Department, University of Waterloo, Ontario, Canada

Three examples of sets of inversive circles

PostScript text file for the above image.
If you have a PostScript interpreter click here to produce the same image using PostScript.

A chain of four touching circles inverted in each other

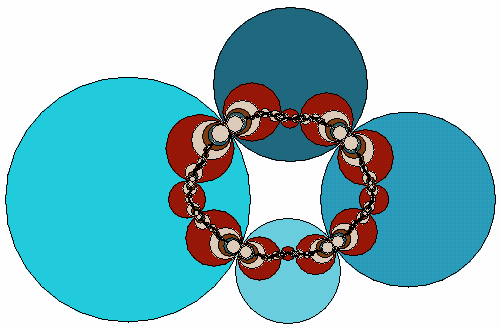
Four mutually touching circles inverted in each other

If you have a PostScript interpreter click here to produce a similar image using PostScript.

A chain of five touching circles inverted in each other

Description

These images are all produced from recursive PostScript programs. They are all formed by repeatedly inverting one circle in another circle. The code below shows how to find the inverse of a point in a circle. More code can be found by looking at the complete PostScript file of the first image.

PostScript Function to Invert a Point in a Circle

/invertPoint
{%def    Invert point xp yp in circle xc yc rc
    %stack before: xc yc rc xp yp
    /yp exch def
    /xp exch def
    /rc exch def
    /yc exch def
    /xc exch def
    /xp xp xc sub def
    /yp yp yc sub def
    rc dup mul
    xp dup mul
    yp dup mul add 
    div dup                  %rc^2/(xp-xc)^2+(yp-yc)^2
    xp mul
    xc add                   %xinvpoint
    exch
    yp mul
    yc add                   %yinvpoint
    %stack after: xinvpoint yinvpoint
} def