x P(x) could also be expressed in any of the following ways.
| Chapter 0: Logic and Proofs |
|---|
In mathematics we are always using sentences involving variables, such as `x 2 > 0.' However, until the value of x is specified, this sentence has no truth value. If we let P(x) denote the sentence `x 2 > 0.' then P(-3) is a true statement and P(0) is a false statement.
If P(x) is a sentence depending on the variable x, we often want to say that P(x) is true for all values of x, or that it is true for at least one value of x. This can be done by adding quantifiers that convert the sentence P(x) into a statement.
x P(x)
where the symbol is called the universal quantifier.
This statement x P(x) could also be expressed in any of the following ways.
If we are dealing with the real numbers, the statement `x, x2 > 0.' means that `For all real numbers x, x2 > 0.' which is a false statement.
However the statement `x, x2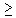 
0.' is true.
x P(x)
where the symbol is called the existential quantifier.
Again this is interpreted to mean that `There exists an x in the universe of discourse for which P(x) is true.'
This statement x P(x) could also be expressed in any of the following ways.
For example, if the universe of discourse is the set of real numbers, then the factorization
x x3 - 1 = ( x - 1 ) ( x2 + x + 1 ) x x2 + x - 6 = 0Solution. If we assume that the universe of discourse is the set of real numbers, we can express this statement as
a x x2 = a.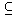
B means that A is a subset of B, and this can be defined using a quantifier as
x ( x 
A => x B ).
If S is a set and Ø denotes the empty set, show that
S 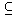S and Ø 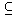S.
Solution.
S 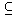S is equivalent to x ( x S => x S ).
If P(x) is the statement x S, then P(x) => P(x) is true for all x. Hence S 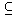S is true.
Ø 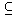S is equivalent to x ( x Ø => x S ). Now x Ø is false for all x. However P => Q is always true if P is false, so that the statement Ø 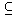S is true.
q ( b = q a )
where the universe of discourse is the set of integers.
Determine whether (i) 0 | 3 and (ii) 0 | 0.
Solution. (i)
0 | 3 is equivalent to q ( 3 = q 0 ); that is,
q ( 3 = 0 ). Since 3 = 0 is always false, 0 | 3 is not true.
(ii)
0 | 0 is equivalent to q ( 0 = q 0 ); that is,
q ( 0 = 0 ). Since 0 = 0 is always true, we can choose q as any integer, and so 0 | 0 is true.
How do we negate quantifiers? For example, the statement `All Canadians speak French.' is not true. However we do not have to show that `All Canadians do not speak French.' to show that the statement is false. We only have to show that `There exists a Canadian who does not speak French.' Similarly, the statement `There exists a real solution to the equation x2=-1.' is false. To show this, we have to show that `For all real x, x2 is not -1.' We have the following rules for negating quantifiers.
| NOT ( x P(x) ) | is equivalent to | ( x NOT P(x) ) | ||
| NOT ( x P(x) ) | is equivalent to | ( x NOT P(x) ) |
As an example of the first rule, ``Not everyone has a calculator'' has the same meaning as ``Someone does not have a calculator.'' As an example of the second rule, ``No one has a calculator'' has the same meaning as ``Everyone does not have a calculator.''
In general, two statements involving quantifiers will be equivalent if they have the same meaning. We cannot always use truth tables to check for equivalence or implications involving quantifiers, so at this stage we have to reason informally to check the equivalence or implication.
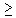x y ( x y ) .
Solution. The statement says that there is a real number x that is greater than or equal to all real numbers. That is, statement says that there is a largest real number. This is false. To show that it is false we have to prove that
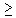x y ( x y ) )
is true. This is equivalent to the following statements.
x NOT ( y ( x y ) ) .
x 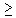y NOT ( x y ) .
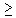x y ( x < y ) .
This last statement is true because, for all x, we can take y = x + 1 .