Next: Calculus of classes: II
Quasi-identities are universal Horn formulas of the form
including the possibility that n=0 and we simply have an equation.
As with identities, we usually omit writing the universal quantifiers.
The study of quasi-identities, and the corresponding model classes called
quasi-varieties, has been pursued mainly in Eastern Europe, following the
lead of Mal'cev. In Western Europe and North America the focus has been
on identities and varieties, a direction initiated by Birkhoff. The rules
for working with quasi-identities are not as simple, or standardized,
as the rules of Birkhoff. Of course the usual rules of first-order logic
suffice to derive all the quasi-identity consequences of a set of
quasi-identities, but one might prefer to have a logical system which
only produces quasi-identities from quasi-identities. One such was
given by Selman [5] in 1972 with four axiom schemes and
six rules of inference. By considering a conjunction
as a set of equations,
rather than an abbreviation for some particular way of inserting
parentheses, we can omit his fifth rule (which handles rearranging
the parentheses and repeat copies of equations):
AXIOMS:
RULES:
.
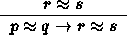We will not go into quasi-identity logic except to make some remarks on the complexity of quasi-identity theories. We note that the quasi-identity theory of a class K of algebras is the same as that of the quasi-variety Q(K) generated by K, as well as of the variety V(K) generated by K. In the latter context the study of quasi-identity theory is better known as the uniform word problem for the variety.
Word problems were one of the first places in mathematics where
mathematicians were able to apply the concepts of algorithm (developed
in the mid 1930's) to obtain undecidability results. Let
be a set of equations in the language
.
Presentations of groups came early in the century in the study of algebraic topology. Of course associated with the presentation one had a group.
.
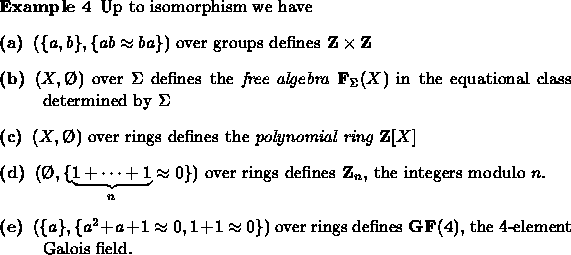
A simple example of a semigroup presentation with unsolvable word problem was found by Tsentin:
Recently A. Mekler,
E. Nelson,
and S. Shelah [4] have proved that there is a finite
such that the word problem for
is unsolvable, but for each
presentation
over
the word problem is solvable.
The use of finite partial algebras is popular in methods for showing the word problem is solvable; in particular the following are equivalent for a variety V:
of a finite partial
algebra
such that
embeds into some member of V.
One can also show that the uniform word problem for V is polynomial time
solvable iff one can find the congruence
in the last item above in
polynomial time. And if the universal theory of
, the relational
version of V, is finitely axiomatizable then the uniform word problem is
solvable in polynomial time. (See Burris [1]].)
An interesting example is that of commutative semigroups, where each finite
presentation
has a word problem solvable
in polynomial time, but the uniform word problem for commutative semigroups is
exponential space complete (due to Mayr & Meyer [3]; see also
Kharlampovich & Sapir [2]).
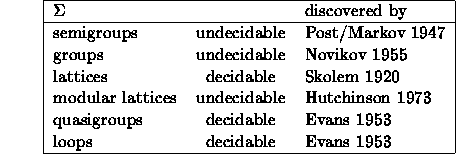
In the table below we give a few examples concerning the solvability of the
word problem for finite presentations.
Rather than give a defining set of equations
it is
simpler to specify the class determined by the intended
.
Next: Calculus of classes: II