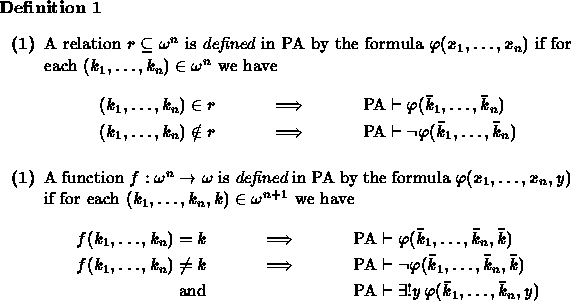
Next: Peano
We return to the two first-order formalizations of arithmetic to make some remarks on how the study of these subjects can be developed further.
Since First-order Arithmetic is known to be rather intractable (it is undecidable), when looking for an effective approach to number theory, something which one might use for an automated theorem prover, it is natural to consider Peano Arithmetic since, as we said, all standard theorems of number theory which can be formulated as first-order statements can be derived from PA. To see that this is true one needs to return to the formulations in the previous section and show that they can be used in PA.
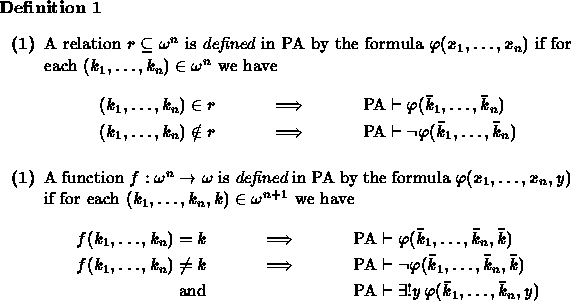
In his 1931 paper Gödel showed that the relations and functions
discussed in the previous section on first-order arithmetic are
indeed definable in PA
.
Using this expressive power of PA Gödel went on to give explicit
first-order sentences which are true in
but cannot be derived from PA.
EXERCISES
Let us briefly review the two versions of the natural numbers which we have considered.
We know from the work of Gödel (1931), Church and Rosser (1936) that
we cannot hope for a reasonable
sound and complete logic to derive all the first-order truths of
number theory. But if we are willing to settle for some of the
truths of number theory we can try PA,
the first-order formulation of Peano's axioms. Then indeed we have
a logic system
which is sound and complete (provided it is consistent); and
all known theorems of traditional number theory which can be expressed
in first-order form can be derived from this system. There are some
very interesting open problems which can be expressed in first-order
arithmetic, e.g., the Riemann Hypothesis. We do not know if these
questions can be settled by Peano Arithmetic -- the completeness is
with respect to all models of PA, not just the nonnegative numbers.