Arithmetic I

First-order arithmetic

Let be the structure , where is the set of non-negative integers. First-order Arithmetic is Th( ), the set of first-order statements in the language which are true in . Much of the fascination of working with first-order number theory comes from the simple fact that there are so many assertions P, including unsolved problems, in number theory for which one can routinely exhibit a specific first-order such that the assertion P is true iff . We say that such assertions can be expressed in first-order arithmetic.

This contrasts sharply with Presburger Arithmetic, i.e., the first-order theory of (Z,+,0,1,<), or the first-order theory for the calculus of classes, i.e., the first-order theory of all structures . For these two examples there are no known unsettled assertions in mathematics for which one can find such a corresponding first-order .

In this section we look at the basic ideas for translating number-theoretic assertions into first-order arithmetic. The starting point is to express some well known relations by first-order formulas.

is an obvious choice for a term to represent the number n.

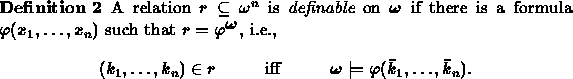
Now we look at a few definable relations:

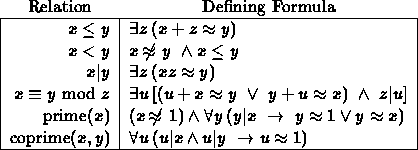
With just these formulas we can express important results, for Euclid's theorem on the infinitude of primes is given by

and Dirichlet's theorem about the infinitude of primes in an arithmetical progression an + b, when a and b are relatively prime, is expressed by

And one can express Goldbach's Twin Prime conjecture by

Many of the results and problems in number theory deal with the exponential function . If we had given ourselves this function as a fundamental operation of then we could easily express Fermat's Last Theorem by

However we do not have this simple situation. Nonetheless we are able to work with a wide class of functions in first-order number theory by defining their graphs.

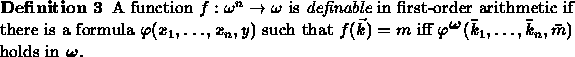
Now, if we could define the exponential function, say by , then we could express Fermat's Last Theorem by

So let us find a way to define exponentiation. The obvious approach is to use recursion (as Dedekind did): and . To compute directly from such a definition we would compute the sequence . However this does not appear to be expressible in first-order form.

For the moment suppose there is a definable function , defined by , such that for each finite sequence there is a b such that . Then we could use to define exponentiation in first-order arithmetic using the following formula :

A beautiful observation of Gödel in his 1931 paper was the fact that one could find such a formula -- however it was simpler to define a certain function of three variables, called Gödel's beta function, given by

where is the remainder after dividing y by x. Clearly is defined by the following formula :

The following lemma says that for any finite sequence from there are numbers b and c from such that is the result of reducing b modulo 1+(i+1)c.

PROOF. Let and let for . Then for p a prime we have , and thus for we have

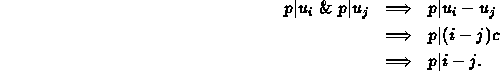
But i-j|c, so p|c, which is impossible. Thus the are pairwise coprime. Consequently by the Chinese remainder theorem one can find an integer b ( ) such that ; and since we have .

So now a slight modification of our attempt (using ) at defining exponentiation succeeds, and we can write a a simple sentence which holds in iff Fermat's Last Theorem is true.

EXERCISES Let DEF be the class of functions definable on (we include the constants as nullary functions).

Peano Arithmetic

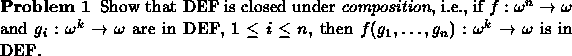
Based on the work of Dedekind and Peano one can give a relatively simple set of first-order axioms, called PA, for the natural numbers from which one can prove all standard theorems of number theory which can be formulated as first-order statements.

PEANO ARITHMETIC

• The language is
• The AXIOMS are
  

  

The standard model of PA is , where the operations are the usual ones. In Example V.14.3 of LMCS we saw that there are other countable models of PA. And once we have developed a derivation calculus then it is possible to return to the sentences in §1 which expressed important assertions and try to prove them by seeing if we can show . This method cannot work all the time by Gödel's incompleteness theorem - and indeed we do not know if PA is strong enough to prove any interesting open problems in number theory.