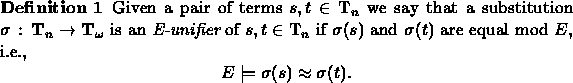
Next: Quasi-identity logic
Just as unification plays a crucial role in the study of term rewrite systems (see Chapter III of LMCS), one has E-unification for work with ETRS's. Indeed the equational theorem prover EQP that William McCune used to verify the Robbin's Conjecture (discussed at the end of Chapter III of LMCS) uses AC-unification.
In the following E will denote a set of equations.
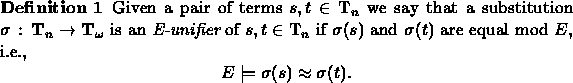
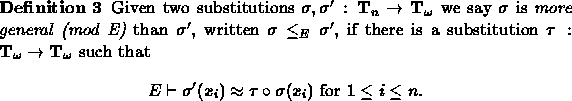
PROOF.\
(Exercise.)
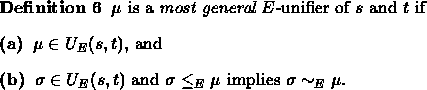
One can no longer assume that an E-unifiable pair has a most general E-unifier -- this depends on the choice of E. The following situations are encountered:
of s and t such that for any E-unifier
of s,t some
is more general than
.
.
of s and t
such that for any
some
is more general than
.
such that no most general unifier of s
and t is more general than
.
This leads to the following unification types:
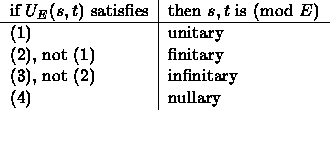
Using this we can give the unification types for sets of equations E:
if every E-unifiable s,t is unitary
if every
E-unifiable s,t
is unitary or finitary, and some
E-unifiable s,t
is finitary.
if every
E-unifiable s,t
is unitary or finitary or infinitary, and some
E-unifiable s,t
is infinitary.
if some
E-unifiable s,t
is nullary.
Rather than working with terms modulo E one can phrase the unification types in terms of the homomorphisms between the free algebras in the variety V defined by E.
Given a term s in
we will adopt the popular convention of using the
same symbol s to denote the corresponding element of
(which is
actually a coset of terms).
The problem of determining if
is the empty set, for
arbitrary terms s,t, is called the
unification problem for E.
This is expressed by the following diagram:
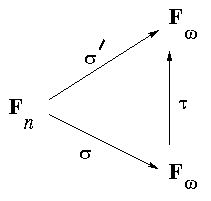
PROOF.
(Exercise.)
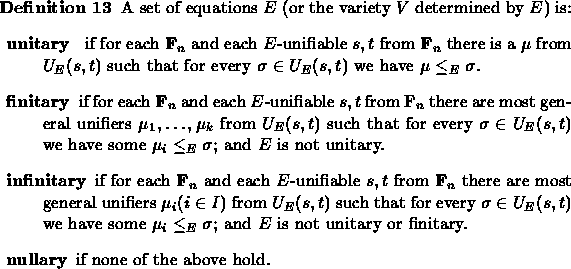
The algebraic approach has proved most useful in determining unification types of some classical theories such as groups -- John Lawrence pointed out the importance of the Hopf and Schreier properties to establish nonnullary type, as we shall see below.
One can also view E-unification as solving equations in
.
Given an equation
, an E-unifier
of s,t
gives a solution
of this equation in
.
And every solution corresponds to an E-unifier.
Thus we can speak of the E-unification type of a single equation.
The unification type of E is then the ``worst'' of
the possible E-unification types of equations
.
One can also generalize this to the E-unification type of a
finite system of equations; and use this to define the unification
type of E. This will agree with the previous type classification,
provided the type is either unitary or finitary. In the examples that follow
the results are the same for these two definitions of the unification type of E.
Solving a system of homogeneous linear equations over
a field
can be formulated in the context of E-unification.
Vector spaces over
can be regarded as an equational
class with the usual vector space operations +,-, the
constant 0, and a collection of unary operations
, for
,
to give the scalar multiplication.
We can axiomatize this
equational theory by the following set E:
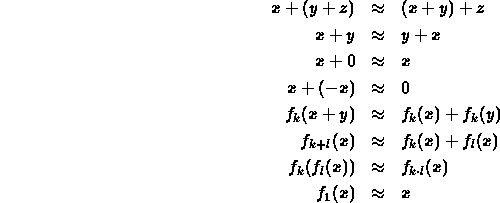
The E-free algebra
is the familiar n-dimensional vector
space
over K, and the substitutions are linear maps.
A particular solution of an
system of homogeneous linear equations
corresponds to a homomorphism
such that each of the left-hand sides of (1) maps to 0. A solution with parameters corresponds to a homomorphism
such that each of the left-hand sides of (1) maps to 0. and in the context of solutions with parameters we can view solutions of a system of homogeneous linear equations as E-unifiers -- the unification type is unitary, and Gaussian elimination solves the unification problem and provides a most general unifier when such exists.
However the above formulation will not suffice to discuss
linear equations in general since the terms in the above language will be
homogeneous,
i.e., of the form
. To remedy this we merely need
to add constants k, for
, to our language, and the following
axioms to E:
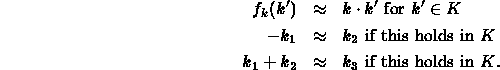
In this setting the E-free algebra
can be thought of as an n+1-dimensional vector-space over
, using the mapping
However the homomorphisms between the free algebras of the equational class defined by E will not correspond to linear maps between the corresponding vector spaces.
A particular solution of an
system of linear equations
corresponds to a homomorphism
such that each of the left-hand sides of (2) maps to 0; and a solution with parameters corresponds to a homomorphism
such that each of the left-hand sides of (2) maps to 0. Solutions with parameters correspond to E-unifiers -- and again the unification type is unitary, and Gaussian elimination solves the unification problem and provides a most general unifier when such exists.
When Plotkin originally proposed that the notion of unification be extended to E-unification in 1972 he presented the example of the associative law for a binary operation -- this of course defines semigroups.
.
Elements of the free semigroups can be conveniently thought of as
strings on an alphabet, and hence we can attach a length
|s| to such strings s.
For
we associate a tuple of
positive integers
Now we observe that for any string s from
we have
.
Consequently, giving
the coordinatewise ordering, for
, (i=1,2), we have
Thus for any infinite descending sequence
there must exist an
such that
Choose
such that
Then for
we have
mapping the variables of the range of
to variables (otherwise
).
Such a
cannot be one-to-one on the variables in the range of
, for otherwise
and
would be
equivalent under
. This leads to the conclusion that the
ranges of
have a strictly
decreasing (finite) number of variables in them. This is impossible,
and hence so is the existence of an infinite sequence (3).
Thus for semigroups we see that the ``more general than'' relation on
Hom(
) has the descending chain property; and thus
the unification type of semigroups cannot be nullary.
Now we turn to an example to show that the
unification type of semigroups is infinitary. Consider the
equation
. Clearly it can be unified; what is not so
obvious is that every unifier
is of the form
for some choice of string s and positive integers i,j.
(This is proved below in Example 16 on groups.)
Furthermore,
every
of the form (4,5) is a unifier. We leave it as
an exercise to show that the most general unifiers of
are
given by (4,5) with s=z, a variable, and
gcd(i,j) = 1. Consequently we have an equation
whose unification type is indeed infinitary.
One of the questions posed by Plotkin in 1972 was how to deal with
situations like E being defining equations for groups. In this case
there is no obvious way to assign a ``length'' to elements of the
free algebras with the property that substitutions are non length
decreasing. (Consider the fact that a simple substitution, of
for y, can reduce
to e.)
The unification type of groups was not determined until 1989, when John Lawrence realized how to use some deep facts about the nature of free groups. His analysis points to the fact that the classification of the type of groups cannot, in all likelihood, be determined by a ``local'' analysis of terms; but rather one needs to know how the terms interact in a global fashion, i.e., some special properties of the free objects. Recall that the size of a set of free generators in a free group is an invariant, called the rank of the free group. (Any variety with a nontrivial finite member has such a rank function.)
Now we give Lawrence's analysis of groups.
Let
be the free group freely generated by
elements. Two key properties are needed:
, if
is not one-to-one then the rank of
is less than n.
Let us first use these properties to show that the
unification type of
is nullary.
Letbe a unifier of
is either 0 or 1. If it is 0 then we have the trivial unifier which maps x and y to e. If it is 1 then we have
and
in a cyclic subgroup of
, so there is an element s of
,
.
Now we leave it as an exercise to show that the most general unifiers of
Thus the type of groups is either infinitary or nullary. It only remains to rule out nullary.
Now suppose we are given some
finite set S of group equations, and suppose that
is not a most general unifier of S.
Then there is a
such that
.
In particular we have a
such that
.
As
is a free group of rank
for some
,
and since
,
we have a
and a
such that
is one-to-one on the range of
is the subgroup of
generated by
.
, we have
.
Now if
is not a most general unifier of S, then by repeating
this process one can
find
and
such that
,
and the range of
is the subgroup of
generated by
. Let
be such that
. Then
maps the range of
onto the range of
, so
cannot be one-to-one
on the range of
(otherwise we could show
). By the Hopf property it follows that
.
Consequently one can only apply the ´ operation above finitely many
times before reaching a most general unifier. This proves groups are
not nullary, and finishes the proof that the type of groups is indeed
infinitary.
Lawrence continues his work on groups to show that most general unifiers
of a finite set S of group equations in the variables
are in one-to-one
correspondence with the the minimal normal subgroups
of
which
identify the left and right hand sides of the various equations in S,
and are such that
is free. Then Lawrence
applies a classical algorithm (of Nielsen) to get a set of free generators,
and this gives an algorithm for
generating the most general unifiers of S. (We note that the
unification problem for groups is trivial -- terms can always be unified.)
An unsolved problem posed by Lawrence is the following.
Will the unification type of any finite set of group equations be either unitary or infinitary?
For any variety of Abelian groups the unification type is unitary. Albert and Lawrence have done a thorough analysis of nilpotent class c groups, for c>1. Such classes are always nullary. Furthermore any finite set of equations is either unitary or nullary, and they have found an algorithm which determines which case holds; and, if the answer is unitary, then it gives the most general unifier.
Commutative rings have been studied by computer scientists (sometimes described as algebras related to Hilbert's Tenth Problem). For commutative rings the free objects are the well-known polynomial rings:
A system of commutative ring equations can be thought of as a system
of Diophantine equations, and unification is concerned with
finding solutions in the above polynomial ring
.
This is actually present in classical number theory, for example the
most general solutions of the Pythagorean equation
have long been known to be the following eight:
and
There is a close tie between solving a set S of commutative ring equations
in the integers
and solving them in the polynomial ring
, namely
iff in
.
is both a subring and a
homomorphic image of the polynomial ring. Consequently the unification
problem for commutative rings is precisely the problem of the
solvability of Diophantine systems in the integers, known as Hilbert's
Tenth problem. Matijasevic, building on the work of Davis, Putnam, and
Robinson, proved that there is no algorithm to determine if a finite
system of Diophantine equations can be solved in the integers.
Consequently the unification problem for commutative rings is
undecidable.
We do not know the exact unification of type of commutative rings, but we have narrowed it down:
To see this we will show that the Pell equation
is infinitary. First we know that (a,b) is a solution in integers iff
for some integer n. Thus there are an infinite number of constant
solutions to (6).
We will show that there are no other
solutions in
, and then it follows that the
constant solutions are all most general,
so the type of (6) is indeed infinitary.
If there is a nonconstant solution
of (6) then there is a nonconstant solution
in only one variable. Now the sequence
has polynomially bounded growth, and it is eventually strictly
increasing. But then it must eventually be a subsequence of
. This is impossible.
Is the unification type of commutative rings infinitary? (I.e., does
every solution of a finite set of Diophantine equations come from a
most general solution?)
Let E be a set of equational axioms for Boolean algebras.
In 1987 Büttner & Simonis proved that the unification type of
E is unitary. To see this let s,t be E-unifiable terms,
and let
be a fixed E-unifier of s,t. Then we claim that
the most general E-unifier of s,t is given by
where + is the usual ``symmetric difference'' of Boolean algebras, since one has
, and
we have
.
In 1990 Nipkow published a proof that the variety determined by a primal algebra has unitary unification type. Such varieties are special cases of discriminator varieties. For definitions, examples, and a proof that discriminator varieties have unitary unification type see [].
A short table of some of the more popular sets of equationally defined classes
follows, with their types (if known):
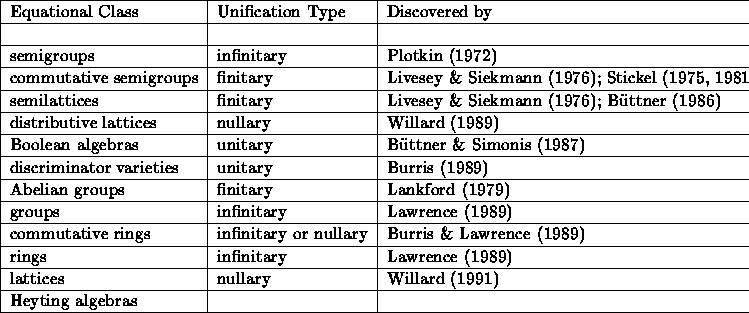
Other recent results include
equational theories of two-element algebras (making use of Post's
classification of the clones on 2 elements).
, that is the language of
rings without the operation minus, then one can write down a
finite set of equational axioms E whose consequences are precisely
the consequences of commutative ring theory which do not mention minus.
Such a system was studied by Franzen in Hilbert's tenth problem
is of unification type zero, J. Automated Reasoning 9 (1992),
169-178, where he shows the unification type is nullary. In spite of the
title of the paper, his result does not resolve the unification type
of commutative rings -- having the minus operation gives a radically
different situation.
EXERCISES
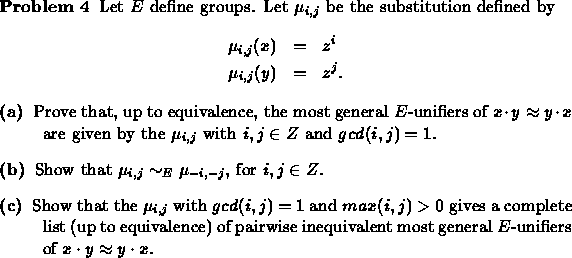
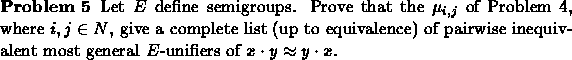
Next: Quasi-identity logic
Fri Jan 31 11:45:40 EST 1997
