Next: Comparing the strentgh of propositional proof systems
In Chapter II of LMCS we looked at the propositional proof system PC and resolution theorem proving. A number of ideas have been developed regarding just how one sets up the basic structure of a proof system. We will look at some of the main ones here.
During the early development of propositional calculi, especially in the Warsaw school of the late 1920's, three basic questions came to the surface -- and in 1946, after Tarski had moved to the U.S., he posed them to his American audience. In the following we assume that we are working with propositional calculi whose only rule of inference is modus ponens, and which have a finite set
of axiom schemata.
is sound and complete?
is an independent set of schemata?
is there an algorithm to determine which propositional formulas are derivable?
In 1949 Lineal & Post [4] answered all three questions in the negative -- such algorithms do not exist for Q1 and Q2, and there is a finite
for which there is no algorithm to determine which formulas can be derived. Perhaps this makes the difficulty of the proof of the completeness of Frege/Lukasiewicz seem a little less surprising.
In the late 1920's Lukasiewicz indicated that he was going to write a comprehensive account of research on the propositional calculi -- obviously such a work would consist of a number of special cases, with no clear pattern of what to expect in a sound and compete calculus.
He was also interested in finding independent sets of schemata, and the method of `matrices' was developed by Bernays and him for this purpose. The basic idea to show that a schema
cannot be derived from
is to find an algebra
,
where S is the set of connectives,
and an endomorphism
such that
has some property
for each substitution instance of each schema different from
is preserved by the rules of inference
does not have
.
In view of the answer to Q2 this method was doomed to be fragmentary. Nonetheless it is quite useful. Let us use it to show:
Example 3 A3 cannot be derived from A1 and A2 in the FL propositional calculus.
We can let A={0,1},
and let the connectives
be associated to the functions:
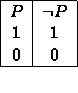
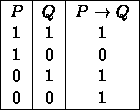
Let
be such that
and
.
Then any instance
of A1 or A2 is such that
.
Also if
then
.
But A3, which is
,
maps to 0 under
,
EXERCISES
Once we have a formal system, i.e., axioms and rules of inference, it is fairly routine to write a program to check if a sequence of formulas is indeed a derivation. And such programs are usually rather fast. The best known example is Automath, developed by de Bruijn in the Netherlands. Automath has been used to check all proofs in Landau's famous elementary book Grundlagen der Analysis. Once one has a proof checker it is straightforward to consider the possibility of using the proof checker to build an automated theorem prover.
The most primitive version of a theorem prover would be to start generating all possible finite strings and check to see which are derivations. Each time we find a derivation we add the conclusion to our bag of theorems. If our formal system is complete then every theorem will turn up sooner or later. However attractive this might sound, we are rapidly defeated by large numbers.
Suppose we have only two symbols, and we want to look at all sequences of at most 10 strings, each string of length at most 10, to see which are derivations. Then we will have
many distinct strings to consider, and then
distinct lists of strings to consider, which is impossible.
The most obvious way to cut down on the time demand is to only look at strings which are well defined formulas for our formal system. Generating well defined formulas is quite straightforward - we can make this simpler by putting some restriction on the number of variables we would like to consider. Then, in the propositional calculus for example, we would take the variables and generate new formulas by closing under the propositional connectives.
In our propositional logics we stated that formulas can be thought of as the terms for the algebra of connectives. So let us give a general recursion for the number of terms of an algebraic system with at most v variables and of length at most l, where we measure the length of a term by putting it in prefix form and counting the number of symbols occurring. Thus if our language has m0 constant symbols and mi function symbols of arity i, for i > 0, then, letting terms(n) be the number of terms of length n, we have:
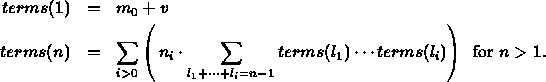
As an example let us look at the
Frege/Lukasiewicz propositional logic. We have
one binary connective
(
)
and one unary connective
(
)
Thus
,
,
, and
for i>2. Using the
above formulas we obtain the following values for terms(n) in the cases
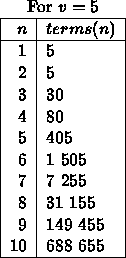
So if we wanted to sift through all lists of at most ten propositional
formulas of length at most 10, even in one variable, we would have
more that
cases, so again we have impossibility. Proof systems
in the propositional calculus offer an alternative to truth tables -
but it seems that if they are to be used for computer theorem proving
then one will need to be clever.
.
If k = 0 we have an axiom, and if k > 0 we have a rule. The preferred approach to substitution (since von Neumann, 1927) is to treat the axioms and rules as schemata, i.e., one is allowed to use any substitution instance of them, but not to use substitution as an rule of inference. (Note that substitution cannot be expressed as a scheme of the above form.) A derivation is then a finite sequence of formulas
such that each
is either an axiom or the result of applying a rule of inference to previous steps. The last step
is the derived formula, and we write
.
The notation
means one has a derivation of
from
,
i.e., the definition of derivation is now extended to permit the appearance of any of the formulas
in the derivation sequence. Any such propositional calculus will be called a
Frege/Hilbert propositional calculus.
We note that since substitution is not expressible as a rule (as defined above) we have the unfortunate situation that Frege's propositional calculus does not qualify as a modern Frege/Hilbert propositional calculus.
Given a Frege/Hilbert propositional calculus we say it is
sound if
,
it is complete if
,
and it is implicationally complete if
.
A Frege system
(see Cook and Rechkow) is an implicationally complete and sound
Frege/Hilbert propositional calculus with an adequate set of
connectives, each of which has at most two arguments (for example
Frege/Lukasiewicz
propositional calculus).
One way to strengthen a Frege system is to permit extension by definitions, i.e., one is allowed to use definitions of the form
in a derivation, where P does not occur in
or any previous step.
Such propositional calculi are called
extended Frege systems.
In extended Frege systems one can find short (i.e., polynomially bounded) derivations of the pigeonhole tautologies.
A second way to strengthen a Frege system is to permit substitution as a rule of inference -- however note that when carrying out a derivation to show
, one does not want to apply substitution to the members of
. This can be handled by treating the propositional variables of
as constants.
The deduction lemma is a powerful tool of everyday mathematics, namely to show
we assume
and prove
.
To incorporate this into our propositional calculus as a rule of inference forces us to modify our notion of what a line of a proof should look like, namely we need to accommodate arbitrary finite sets
of propositions
to express the deduction rule:
.
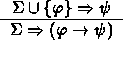Note that we have replaced
by a new symbol
which is now a part of our formal language. A
(natural deduction) line
is an expression
, where
is a finite (possibly empty) set of formulas. A derivation is a finite sequence of natural deduction lines, each of which is either an axiom or results from applying a rule of inference to previous members of the sequence. A derivation of a formula
is a derivation
whose last member is the natural deduction line
.
The following is an example of a natural deduction propositional calculus obtained from Frege/Lukasiewicz propositional calculus:
AXIOMS:
(1)
(2)
(3)
RULES OF INFERENCE:
(1)
(2)
(3)
.
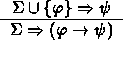Similarly one can transform any Frege/Hilbert propositional calculus into a natural deduction propositional calculus.
One can define the notions of sound, complete and implicationally complete in an obvious manner, namely sound means
,
complete means
,
and implicationally complete means
,
Cook and Reckhow define a
natural deduction system
to be a natural deduction propositional calculus which has a finite number of axioms and rules, an adequate set of connectives, and is sound and implicationally complete (such as the example above).
.
where
and
are finite sets of formulas.
The intended interpretation is that
an evaluation which makes all members of
true will make some member of
true.
A derivation is a finite sequence of sequents such that each member is either an axiom or the result of applying one of the rules of inference to previous members. We will call such a propositional calculus a Gentzen propositional calculus.
Such a calculus is sound if
,
complete if
,
and implicationally complete if
,
A Gentzen system
is a Gentzen propositional calculus which has an adequate set of connectives, is sound and implicationally complete.
One obvious way to obtain a Gentzen system is to take a natural deduction system and replace natural deduction lines in the axioms and rules of deduction by sequents, e.g., replace
by
.
Gentzen made use of the popular, and powerful,
cut
rule:CUT
Previous: An algorith to find derivations in PC
Next: Comparing the strentgh of propositional proof systems
Fri Jan 31 11:06:28 EST 1997