Clones

As we have seen in II.5 of LMCS, different collections of connectives can have quite different expressive power. An obvious measure of the expressive power of a set of connectives is to take all formulas which can be built out of them, along with their associated truth-tables. However, if we are only interested in the expressive power up to truth-table equivalence, then it suffices just to take the set of truth-tables associated with the formulas. This leads to the notion of a clone.

Thus, for example, we can now say that a set S of connectives with truth-tables X is adequate for the classical propositional calculus if .

A finite algebra which has the property that its clone is all functions on A is called a primal  algebra. In II.5.1 of LMCS we essentially pointed out that the two-element Boolean algebra is a primal algebra. One can easily show that the finite fields GF(p), p a prime, are primal. It is not known if one can test a finite algebra for primality in polynomial time.

EXERCISES

Duality

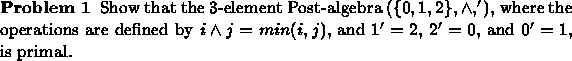
We want to define the notion of dual functions for finitary functions on the set {0, 1}. So consider . The dual  of f is the function obtained by interchanging 1 and 0 in the arguments and values of f, i.e.,

We say that a function is self-dual  if it is equal to its dual.

Two connectives are said to be dual if their associated truth-tables are dual, and a connective is self-dual if it is its own dual.

For X a set of finitary functions on {0,1} we define to be the set of duals of members of X.

PROOF. It suffices to show that dual and composition commute. But this is easy:

Post's classification of 2-valued logics

Emil Post  classified all possible clones on {0,1}, and hence in a natural sense all possible 2-valued propositional logics. His work was first presented in 1920 as a companion piece to his Ph.D. Thesis, and it was finally published in the book Two-valued Iterative Systems of Mathematical Logic, Princeton, 1941. The classification of E. Post  was presented in a more modern notation by R. Lyndon (see [3]).

Post 's classification of clones on {0, 1} consisted in giving a set of generating functions for each clone. One consequence of his classification is that each clone on {0, 1} is finitely generated . We will give a list of bases for the clones following Lyndon. (Clones come in dual pairs, and only one member of each such pair will be given.)

We will take as our building blocks the constants

0, 1;

the truth-tables of the standard connectives

;

the function + defined by

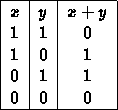
the function (x, y, z) defined by

;

the function [x, y, z] defined by

;

and the functions , for , defined by

where the notation means that is omitted.

Now we are ready to give a basis (up to duality) for each of the countably many clones on {0, 1}:

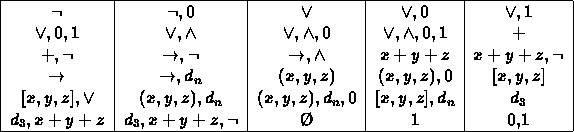
Post  (1921/1941) suggested that n-valued logics be considered. However one cannot give such a nice classification even for the 3-valued iterative systems since there are continuum many. [See Janov  & Mucnik  ([2] 1959) Hulanicki  & Swierczkowski  ([1] 1960).] Connectives in n-valued logic can again be thought of as components in circuits. In multi-valued logic one of the interests is to find good components for designing circuits.

Can one classify the finitely generated 3-valued systems?

Post notes the intractability of classifying iteratively closed sets of propositional formulas (there are continuum many). If denotes such a closure, he asks if there is an algorithm to determine for finite if .

EXERCISES

References

1

A. Hulanicki and S. Swierckowski, Number of algebras with a given set of elements. Bull. Acad. Polon., Sci. Sér. Sci. Math. Astronom. Phys. 8 (1960), 283-284.

2

Ju.I. Janov and A.A. Muchnik, On the existence of k-valued closed classes that have no bases. (Russian) Dokl. Akad. Nauk SSSR 127 (1959), 44-46.

3

R. Lyndon, Identities in two-valued calculi. Trans. Amer. Math. Soc. 71 (1951), 457-465.

4

E. Post, Introduction to a general theory of elementary propositions of logic. Amer. J. Math. 43 (1921), 163-185.