Next: Frege
As we have seen, the naive use of classes, in particular the connection between concept and extension, led to contradiction. Frege mistakenly thought he had repaired the damage in an appendix to Vol. II. Whitehead & Russell limited the possible collection of formulas one could use by typing. Another, more popular solution would be introduced by Zermelo. But first let us say a few words about the achievements of Cantor.
We include Cantor in our historical overview, not because of his direct contribution to logic and the formalization of mathematics, but rather because he initiated the study of infinite sets and numbers which have provided such fascinating material, and difficulties, for logicians. After all, a natural foundation for mathematics would need to talk about sets of real numbers, etc., and any reasonably expressive system should be able to cope with one-to-one correspondences and well-orderings.
Cantor started his career by working in algebraic and analytic number theory. Indeed his PhD thesis, his Habilitation, and five papers between 1867 and 1880 were devoted to this area. At Halle, where he was employed after finishing his studies, Heine persuaded him to look at the subject of trigonometric series, leading to eight papers in analysis.
In two papers 1870/1872 Cantor studied when the sequence
converges to 0. Riemann had proved in 1867 that if this happened on an interval and the coefficients were Fourier coefficients then the coefficients converge to 0 as well. Consequently a Fourier series converging on an interval must have coefficients converging to 0. Cantor first was able to drop the condition that the coefficients be
Fourier coefficients -- consequently any trigonometric series convergent on an interval had coefficients converging to 0. Then in 1872 he was able to show the same if
the trigonometric series converged on
, provided
, where
is the
derived set of A. The sequence of derived sets is monotone decreasing, and by taking intersections at appropriate points
he was led in 1879 to introduce the ordinal numbers
. The key property of ordinals is that they are well-ordered sets. (A well-ordered set can be order embedded in the real line iff it is countable.)
We have already mentioned Cantor's (brief) 1872
description of how to use Cauchy
sequences of rationals to describe the reals.
He says that identifying the geometric line with the reals is an axiom.
Cantor's first results on cardinality appear in an 1874 paper where he introduces the 1-1 correspondences, and uses them to show that the algebraic numbers can be put in 1-1 correspondence with the natural numbers; and in the same paper he proves that such a correspondence between any interval of reals and the natural numbers is not possible. Thus he has a new proof of Liouville's 1844 result on the existence of (infinitely many) transcendental numbers (in every interval).
In 1878 Cantor proved the (at that time quite paradoxical) result that
could be put into 1-1 correspondence with the reals. He wrote to Dedekind saying
I see it, but I don't believe it.
Cantor subsequently tried to show that no such correspondence could be a homeomorphism if n > 1, but a correct proof would wait till Brouwer (1910).
Next followed Cantor's publications of a series of six papers,
On infinite sets of reals,
written between 1879-1884, in which he refined and extended his previous work on infinite sets. He introduced countable ordinals
to describe the sequence of derived sets
, and proved that the sequence would eventually stabilize in a perfect set. From this followed the result that any infinite
closed subset of
is the union of a countable set and a perfect set. Next he proved that any nonempty perfect subset of R could be put in one-to-one correspondence with the real line, and this led to the theorem that any infinite closed set was either countable or had the cardinality of the real line. Cantor claimed that he would soon prove every infinite subset of
had the cardinality of the positive integers or the cardinality of
, and thus the cardinality of
would be the second infinity. His proof of what would later be called the
Continuum Hypothesis
(more briefly, the CH)
did not materialize. Later Souslin would be able to extend his ideas to show that analytic sets were either countable or the size of the continuum; attempts to settle the Continuum Hypothesis would lead to some of the deepest work in set theory -- by Gödel (1940), who showed the consistency of the CH, and Cohen (1963) who invented forcing to show the independence of the CH.
A particularly famous result appeared in
On an elementary problem in the study of manifolds
(1890), namely the set of functions
, i.e., the set of functions from A to {0,1},
has a larger cardinality than A, proved by the now standard diagonal method.
Cantor's last two papers on set theory,
Contributions to the foundations of infinite set theory,
1895/1897, give his most polished study of cardinal and ordinal numbers and their arithmetic. He says that the cardinality of a set is obtained by
using our mental capacity of
abstraction,
by ignoring the nature of the elements. By looking at the sequence of
sizes of ordinals he obtains his famous
's
(
) which,
ordered by their size, form a well-ordered set
in the extended sense,
i.e., for any set of
's there is a smallest one, and a next largest one.
He claims that the size of any set is one of his
's -- as a
corollary it immediately follows that the reals can be well-ordered.
He tried several times to give a proof of this claim about the
's; but it was not until 1904, when
Zermelo invoked the axiom of choice, that there would finally be a success.
For his development of ordinal numbers he first looks at
linearly ordered
sets and defines + and
for the
order types
abstracted from them. Next he shows the order type of the rationals is completely determined by the properties of being
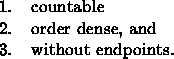
Then he characterizes the order type of the interval [0,1] of reals by
Ordinals
are then defined as the order types (abstracted from) well-ordered sets. Exponentiation of ordinals is defined, and the expansion of countable ordinals as sums of powers of
is examined. The paper ends with a look at the countable
ordinals, i.e., those
which satisfy
(and hence their expansion is just
).
By the end of the nineteenth century Cantor was aware of the paradoxes one could encounter in his set theory, e.g., the set of everything thinkable leads to contradictions, as well as the set of all cardinals and the set of all ordinals. Cantor solved these difficulties for himself by saying there were two kinds of infinities, the consistent ones and the inconsistent ones. The inconsistent ones led to contradictions. This approach, of two kinds of sets, would be formalized in von Neumann's set theory of 1925.
Cantor's early work with the infinite was regarded with suspicion, especially by the influential Kronecker. However, with respected mathematicians like Hadamard, Hilbert, Hurwitz, Mittag-Leffler, Minkowski, and Weierstrass supporting his ideas, in particular at the First International Congress of Mathematicians in Zürich (1897), we find that by the end of the century Cantor's set theory was widely known and publicized, e.g., Borel's Lecons sur la théorie des fonctions was mainly a text on this subject. When Hilbert gave his famous list of problems in 1900, the Continuum Problem was the first.
A considerable stir was created at the Third International Congress
of Mathematicians in Heidelberg (1904) when König presented a
proof that the size of
was not one of the
's of Cantor.
Cantor was convinced that the cardinal of every set would be one of
his
's. König's proof was soon refuted.
The first textbook explicitly devoted to the subject of Cantor's set theory was published in 1906 in England by the Youngs, a famous husband and wife team. The first German text would be by Hausdorff in 1914.
Next: Frege
Fri Jan 31 13:33:38 EST 1997