Previous:
Feasible Computations
Next:
A proof of Boole's Elimination Theorem
Up: Supplementary Text
A proof of Boole's Expansion Theorem
[Theorem 1.4.3 of LMCS]
Given classes 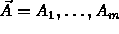 we say K
is an
we say K
is an
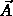 -constituent
if it is a constituent for the classes
-constituent
if it is a constituent for the classes
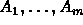 .
Boole used the following theorem to
expand
a given expression
.
Boole used the following theorem to
expand
a given expression
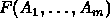 into its constituents.
It says basically that
F is a union of
into its constituents.
It says basically that
F is a union of 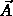 -constituents, and a given
-constituents, and a given 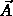 -constituent
K is a constituent of this expansion of F if and
only if
-constituent
K is a constituent of this expansion of F if and
only if 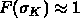 , where
, where 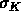 is the unique sequence
is the unique sequence  of 1's and 0's that make
of 1's and 0's that make 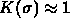 . The following gives the
. The following gives the 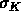 for the constituents belonging to the three classes A,B,C:
for the constituents belonging to the three classes A,B,C:
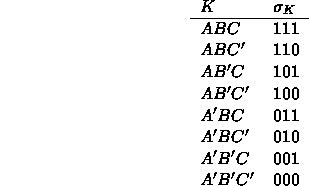
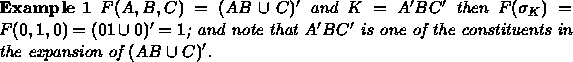
Note that if K,L are both 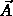 constituents then
constituents then
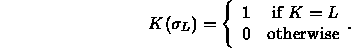
Theorem [Expansion Theorem]
Let 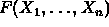 be given. Then
be given. Then
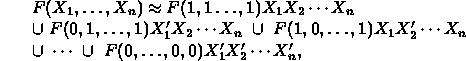
or, more briefly,
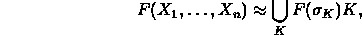
where K ranges over the 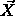 -constituents.
-constituents.
Proof
By using the fundamental identities on page 11 one sees
that it is possible to express F as a union of constituents.
So we write
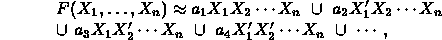
where each constant 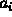 is either 0 or 1.
We can write this more briefly as follows (using the fact that there
are
is either 0 or 1.
We can write this more briefly as follows (using the fact that there
are 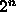 constituents for n variables)
constituents for n variables)
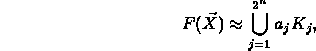
where the 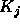 are the various
are the various 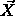 -constituents.
-constituents.
Now one observes that for 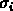 being the unique sequence of 1's and 0's
that gives
being the unique sequence of 1's and 0's
that gives 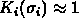 , i.e.,
, i.e., 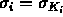 , we have
, we have

as desired.
Previous:
Feasible Computations
Next: A proof of Boole's Elimination Theorem
Up: Supplementary Text
Stan Burris
Fri Jan 31 17:59:12 EST 1997
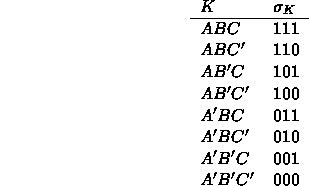
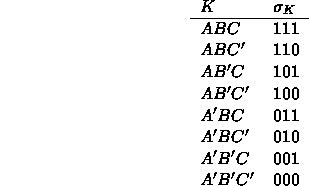
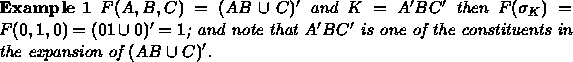
![]() constituents then
constituents then
![]()
![]()
![]() -constituents.
-constituents.
![]()
![]() is either 0 or 1.
We can write this more briefly as follows (using the fact that there
are
is either 0 or 1.
We can write this more briefly as follows (using the fact that there
are ![]() constituents for n variables)
constituents for n variables)
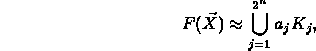
![]() are the various
are the various ![]() -constituents.
-constituents.
![]() being the unique sequence of 1's and 0's
that gives
being the unique sequence of 1's and 0's
that gives ![]() , i.e.,
, i.e., ![]() , we have
, we have
