A Family of Conics Associated with
the Configuration of Pappus

Leroy J. Dickey

Table of Contents

T_o_C

• List of Figures
• Abstract
• Part 1
  • The constructions
    • The Base Figure
    • The Six Conics Q(X)
  • The Theorem
  • The proof
    • The outline
    • The details
• Part 2
  • Notation: The Pappus configuration and Pappus Line P(X,Y,Z; U,V,W)
  • The Steiner points S_e and S_o
  • The twelve Steiner conics Q_e(X) and Q_o(X)
  • The connection between Q(X) and the two Steiner conics Q_e(X) and Q_o(X)

List of Figures

T_o_C

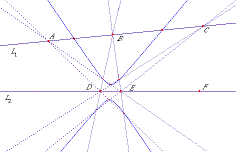
• Figure 1. The conic Q(F).
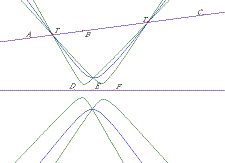
• Figure 2. The three conics Q(D), Q(E) and Q(F) meet L₁ at T₁ and T₂.
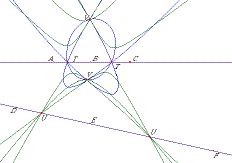
• Figure 3. All six conics: Q(A) Q(B), Q(C), Q(D), Q(E) and Q(F).
• Figure 4. A Steiner conic associated with the configuration of Pappus.

Abstract

T_o_C

In this paper, we show a family of six conics connected with the Configuration of Pappus. These conics meet in interesting ways. There are two points on one of the base lines that are common to three of the conics. There are two points on the other base line that are common to the other three conics. There are two further points that are common to all six conics. These six points together with the intersection of the two base lines form a complete quadrangle. In the second part of this paper, we show the connection between the above six conics and 12 Steiner conics that are connected with the configuration of Pappus.

The construction

T_o_C

• The Base Figure
  • Let L₁ and L₂ be two distinct (base) lines.
  • Let O be the point of intersection of the two base lines L₁ and L₂.
  • Let A, B and C be three points on the line L₁ that are distinct from each other and distinct from O.
  • Let D, E and F be three points on the line L₂ that are distinct from each other and distinct from O.
• The Six Conics
  We construct six conics, Q(A), Q(B) Q(C), Q(D) Q(E) and Q(F) as follows:
  • Let S = { A, B, C, D, E, F }.
  • For each point X in S, construct a conic Q(X) as follows:
    • Let S(X) be the five points in S \ { X }.
    • Let S₀(X) be the set of three points in S(X) that are on the line (either L₁ or L₂) not containing X.
    • Let S₀(X) = S(X) - S₁(X).
    • Construct the six lines connecting the 3 points in S₁(X) to the 2 points in S₂(X).
    • These six lines meet in eleven distinct points. Five of the eleven are in S. The remaining six points lie on a conic that we call Q(X), for X = A, B, C, D, E, or F.
    • ( Figure 1 shows the particular conic Q(F). )

 
Figure 1, The conic Q(F)
More about Figure 1.
List of Figures

The Theorem

T_o_C

• There are two points, T₁ and T₂ on the line L₁ that the lie on all three conics Q(D), Q(E) and Q(F).
• There are two points, U₁ and U₂ on the line L₂ that lie on all three conics Q(A), Q(B) and Q(C).
• There are two points, V₁ and V₂, that are diagonal points of the complete quadrangle T₁, T₂, U₁, U₂ and lie on all six conics.

The outline of the proof

T_o_C

• Set up the coordinates for the Base Figure.
• Find the equations of the Six Conics Q(A), Q(B), Q(C), Q(D), Q(E) and Q(F).
• Find the coordinates of T₁ and T₂, the two points of intersection of L₁ with Q(F).
• Verify that points T₁ and T₂ are on the conic Q(D).
• Verify that points T₁ and T₂ are on the conic Q(E).
• ( Figure 2 shows three conics Q(D), Q(E) and Q(F) and how they meet at the two points T₁ and T₂ on L₁. )

 
Figure 2: The three conics Q(D), Q(E) and Q(F)
meet L₁ at T₁ and T₂.
More about Figure 2.
List of Figures

• Find the coordinates of U₁ and U₂, the two points of intersection of L₂ with the conic Q(C).
• Verify that points U₁ and U₂ are on the conic Q(A).
• Verify that points U₁ and U₂ are on the conic Q(B).
• Let V₁ be the point of intersection of lines T₁ U₁ and T₂ U₂
• Let V₂ be the point of intersection of lines T₁ U₂ and T₂ U₁
• Verify that both V₁ and V₂ are on all Six Conics.
• ( Figure 3 shows the Six Conics and how they meet by threes at T₁, T₂ and U₁, U₂, and how they all meet at V₁ and V₂. )

 
Figure 3. All six conics: Q(A), Q(B),
Q(C), Q(D), Q(E) and Q(F).
More about Figure 3.
List of Figures

The details of the proof

T_o_C

• The data (source)
  This file contains the Maple V source code giving the coordinates for the six points of the base figure. All other calculations are based on these six points.
• The functions (source)
  This file contains the Maple V source code for seventeen functions that are used to construct all the other objects of this construction, whether they be points, lines or conics.
• The defined objects
  • The Maple V source code for the constructions.
  • The new objects consist of the equations of conics and coordinates of new lines and points.
• The proof (validation of incidences).
  • The Maple V source code for the validations.
  • The results.
    The results of the validation section. All claimed incidences are as they should be.

The Pappus configuration

T_o_C

The Steiner points

T_o_C

• S_e, the "even" Steiner point.
  • The three Pappus lines
    • P(A,B,C; D,E,F),
    • P(A,B,C; E,F,D) and
    • P(A,B,C; F,D,E)
    coincide at a point denoted by S_e.
  • The subscript "e" is used because the ordered sequences (D,E,F), (F,D,E) and (E,F,D) are the three even permutations of the three symbols D, E and F.
• S_o, the "odd" Steiner point.
  • The three Pappus lines
    • P(A,B,C; F,E,D),
    • P(A,B,C; D,F,E) and
    • P(A,B,C; E,D,F)
    coincide at a point denoted by S_o.
  • The subscript "o" is used because the ordered sequences (F,E,D), (D,F,E) and (E,D,F) are the three odd permutations of the three symbols D, E and F.

Twelve Steiner conics

T_o_C

For simplicity, we deal specifically with the particular choice X=F, and the other cases for A, B, C, D and E are similar.

• Consider F as a control point (parameter) allowed to move along on the entire line L₂.
  • The Pappus line P(A,B,C; D,E,F) contains the three points:
    • BF.CE
    • CD.AF
    • AE.BD
  • Two of these points depend on F but AE.BD does not. Hence P(A,B,C; D,E,F) turns on AE.BD.
  • There is a location of F on the line L₂ for which S_e coincides with AE.BD, namely the point where L₂ intersects the line that joins C and AE.BD.
  • Hence the locus of S_e(F) includes the point AE.BD.
  • (summary) The pappus line P(A,B,C; D,E,F) turns on the point AE.BD. (also contains BF.CE and CD.AF ) (F = L2 . C (AE.BD) implies So = AE.BD.)
     
    

    ----=x=O=x=---- ----=x=O=x=---- ----=x=O=x=----
    
     
    

  • The Pappus line P(A,B,C; E,F,D) contains the three points:
    • BD.CF
    • CE.AD
    • AF.BE
  • Two of these points depend on F but , CE.AD, does not.
  • There is a location of F on the line L₂ for which S_e coincides with CE.AD, namely the point where L₂ intersects the line that joins C and BD.AE.
  • Hence the locus of S_e(F)includes the point BD.AE.
  • the third point, CE.AD, is independent of F. Two of the three points depend on F and move as a function of F. turns on the point CE.AD, that is independent of F.
  • There is one location of F, on L₂, namely the point where L₂ intersects the line which joins C and BD.AE, for which S_e is BD.AE. Hence the locus of S_e(F)includes the point BD.AE.
  • In summary, the pappus line P(A,B,C; D,E,F) turns on the point AE.BD. (also contains BF.CE and CD.AF ) (F = L2 . C (AE.BD) implies So = AE.BD.)
  • The pappus line P(A,B,C; F,D,E) turns on the point BE.CD. (also contains AD.BF AND AE.CF) (F = L2 . A (BE.CD) implies So = BE.CD )
  • The pappus line P(A,B,C; E,F,D) turns on the point CE.AD. (also contains AF.BE and BD.CF) (F = L2 . B (CE.AD) implies So = CE.AD )
  • Notable: The three lines
    • A(BE.CD),
    • B(CE.AD) and
    • C(AE.BD)
    coincide. Moreover, if F = L1 . L2, then Se is at this point of coincidence.
• As a function of F, The locus of S_o, is a conic that contains the five distinct points D, E, AE.BD, BE.CD, CE.AD, no three of which are collinear.
• This conic is denoted by Q_o(F) and is defined by the five points D, E, AE.BD, BE.CD, CE.AD .
• Figure 4 shows this conic and three Pappus lines meeting at the Steiner point S₀.

 
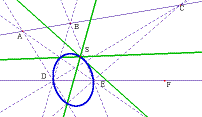
Figure 4. A Steiner conic S_e(F) associated
with the configuration of Pappus.
More about Figure 4.
List of Figures

• Similarly, the three Pappus lines P(A,B,C; D,F,E), P(A,B,C; F,E,D) and P(A,B,C; E,D,F) meet at a second Steiner point, S₁, whose locus, as a function of F, is a second conic that contains the five points D, E, AD.BE, BD.CE, CD.AE.
• This locus is the conic defined by the five points D, E, AD.BE, BD.CE, CD.AE .
• Take the union of the two sets of five points discovered above,
  

  { D, E, AE.BD, BE.CD, CE.AD } and
  { D, E, AD.BE, BD.CE, CD.AE }

  and remove the two points of S₂(F), (namely D and E), to obtain the set of six points { AE.BD, BE.CD, CE.AD, AD.BE, BD.CE, CD.AE }. All six of these points lie on the conic Q(F). [Pascal]

The Connection between Steiner Conics and Q(A), Q(B), Q(C), Q(D), Q(E), Q(F)

T_o_C

• In the same way, for any X in the set S, the loci of the two Steiner points S₀ and S₁, as a function of X, (the conics Q₀(X) and Q₁(X), respectively) lead us to six interesting points, any five of which determine / characterize the conic Q(X). This brings us full circle back to the beginning of the paper.

The end.

T_o_C