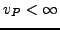, weak duality
holds in general, i.e. the optimal value of
the Lagrangian dual provides a lower bound,
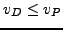. However,
strong duality (i.e.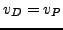 
and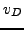 
is attained)
requires a constraint qualification, CQ, e.g. the Slater (strict
feasibility) CQ.
In the absence of a CQ, the dual optimal value 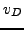may be unattained
and/or there can be a positive duality gap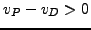 
.
In addition, the (near) absence of a CQ results in numerical difficulties.
We study conditions that guarantee a finite positive duality
gap
.
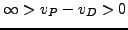Necessary and sufficient conditions for a finite nonzero duality gap
are given, and it is shown how these can be used to generate instances
satisfying this property.
We then present an algorithm that solves in an efficient and stable
way, feasible conic convex optimization problems, including those
for which the Slater constraint qualification fails.
In addition, we illustrate the close relation between strict
complementarity and duality gaps.