|
|
|
|
|
|
| .... |
|
.... |
|
|
World TSP National TSPs VLSI TSPs CIA Factbook GEOnet Server GNIS Data  TSP Links
|
|
The best reported tour for the World TSP has length 7,515,755,956, found on February 15, 2021 by Keld Helsgaun using a variant of his LKH heuristic algorithm, starting with a tour of length 7,515,767,286, found by Xavier Clarist on February 11, 2021. These results together made a major improvment on earlier records, lowering the previous best known tour length by 14,628 meters. To put it in perspective, note that from October 2011 through June 2020, the record was only improved by 7604 meters. The two new tours are available as gzipped files in TSPLIB format: world.7515755956.tour.gz and world_7515767286.tour.gz. The new results break Clarist's old record of 7,515,770,584, found on June 22, 2020, and an earlier record tour of length 7,515,772,107 found by Helsgaun on March 13, 2018. Previous records by Helsgaun were 7,515,772,212 (May 24, 2013), 7,515,778,188 (October 25, 2011), 7,515,786,987 (April 4, 2011), 7,515,796,609 (May 4, 2010), 7,515,877,991 (May 12, 2009), 7,515,947,511 (November 27, 2008), and 7,517,285,610 (September 16, 2003). An older record tour of length 7,518,425,642 was found by Hung Dinh Nguyen, Ikuo Yoshihara, Kunihito Yamamori, and Moritoshi Yasunaga (June 2, 2003), using a combination of iterated Lin-Kernighan and a parallel hybrid genetic algorithm. The current best lower bound on the length of a tour for the World TSP is 7,512,218,268. This bound was established by the Concorde TSP code (June 5, 2007), using CPLEX as a linear-programming solver. The bound shows that Keld Helsgaun's tour has length at most 0.0471% greater than the length of an optimal tour. We will be most happy to report any improved tour or improved lower bound that you may find. Data (Gzipped TSPLIB Format, world.tsp.gz, 11.5 mbytes) 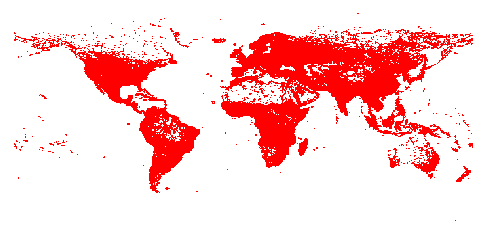
Back to TSP home.
|