We describe below the computations used to solve the 24,978-city Sweden TSP. The majority of the work was carried out on a cluster of 96 dual processor Intel Xeon 2.8 GHz workstations at Georgia Tech's School of Industrial and Systems Engineering, running as a background process when the machines were not otherwise active.
The initial application of the cutting-plane procedure established a linear programming (LP) lower bound of 855,391.17; this bound proved that no tour could be more than 0.0241% shorter than the 855,597 tour found by LKH. The progress of the LP bound in the the cutting-plane run is described in the following table, where each line corresponds to a pass of our cutting routines using increasingly larger maximum "chunk size" in our local cuts algorithm.
| Local Cut Size | LP Bound | Optimality Gap |
| 16 | 855240.70 | 0.0417% |
| 20 | 855283.90 | 0.0367% |
| 24 | 855323.88 | 0.0319% |
| 28 | 855355.87 | 0.0282% |
| 32 | 855372.12 | 0.0263% |
| 36 | 855376.33 | 0.0258% |
| 40 | 855389.25 | 0.0243% |
| 44 | 855389.48 | 0.0243% |
| 48 | 855391.17 | 0.0241% |
We used the final LP produced by this cutting-plane run to start a branch-and-cut process. In the following figure we show the first four levels of the search tree we created by repeatedly subdivding the problem and apply the cutting-plane algorithm to each of the resulting subproblems. In this figure the nodes represent the subproblems and the height of a node corresponds to the bound we obtained with cutting planes.
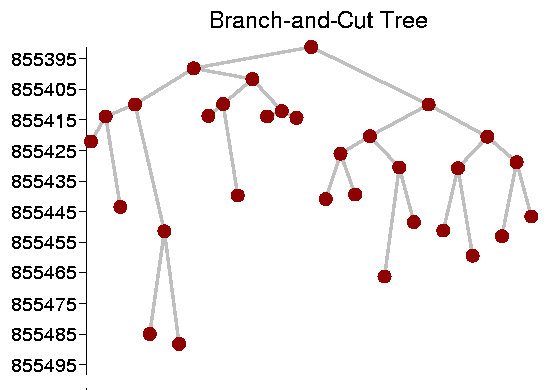
We allowed the tree to grow to 2,011 nodes (this left just over 1,000 active tree nodes that were waiting for processing). In this way we pushed the lower bound up to 855,493, improving the optimality gap to 0.0122%. The full search tree can be found at the tree1 page.
Together with the improved bound, this first branch-and-cut run produced a collection of 102,888 cutting planes (not counting subtour inequalities) at the nodes of the search tree. Since our search for cutting planes is heuristic in nature, it was possible that some of these 102,888 cuts were violated by the optimal solution to our starting LP. Indeed, by applying this collection of cuts and continuing our cutting-plane procedure we were able to improve the starting LP relaxation to 855456.85, giving an optimality gap of 0.0164%.
With this nice improvement in the initial LP bound, we decided it was worthwhile to make a second branch-and-cut run starting with the improved LP. This time, letting the tree grow to 2,965 nodes, we obtained a bound of 855,528 for an optimality gap of 0.0081%.
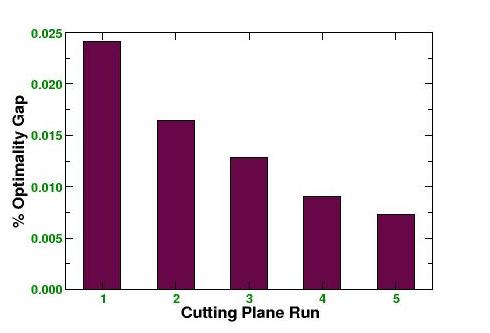
We repeated this process a total of four times, making use of the ever-growing collection of cutting planes to continue to improve the LP relaxations. The optimality gaps for the five resulting LP bounds are give in the following chart.
A summary of the branch-and-cut runs we made with each of these five LP relaxations as the starting (or "root") node is presented in the following table. The "Nodes" column gives the total number of nodes in the branch-and-cut tree, the "Active" column gives the number of active nodes when the process was terminated, and the "Local Cuts" column gives the maximum size of local cuts that were used in the subproblems of the branch-and-cut run.
| Run | Bound | Gap | Nodes | Active | Local Cuts |
| 1 | 855493 | 0.0122% | 2,011 | 1,006 | 32 |
| 2 | 855528 | 0.0081% | 2,965 | 1,482 | 36 |
| 3 | 855579 | 0.0021% | 10,355 | 4,634 | 40 |
| 4 | 855583 | 0.0016% | 14,367 | 5,886 | 44 |
| 5 | 855597 | 0.0000% | 167,263 | 0 | 48 |
The fifth branch-and-cut run is the one that finally solved the Sweden TSP.
Pictures of the branch-and-cut trees for each of the five runs can be found by following the links in the table given below. The full pictures are a bit crowded given the large number of nodes in the trees; to see just the first 5 levels of the branch-and-cut trees follow the links in the "First 5 Levels" column.
| Run | Full Tree | First 5 Levels |
| 1 | tree1 | tree1-low |
| 2 | tree2 | tree2-low |
| 3 | tree3 | tree3-low |
| 4 | tree4 | tree4-low |
| 5 | tree5 | tree5-low |
The cumulative CPU time used in the five branch-and-cut runs and in the cutting-plane procedures for the five root LPs was approximately 84.8 CPU years on a single Intel Xeon 2.8 GHz processor. Details of the computation times are given on the CPU Time page.
We began the initial cutting-plane procedure on the first LP in March 2003 and the final branch-and-cut run finished in January 2004. After the run completed, we made a final check of the 14,827,429 cutting planes (besides subtour inequalities) that were generated and used during the process. This final checking was completed in May 2004.
The total computation for the Sweden TSP makes it one of the largest efforts to date to solve an optimization problem. We can expect that more powerful computational platforms in the future will permit the study of even larger instances, but further progress in the solution of the TSP will no doubt depend much more heavily on improved algorithmic techniques than improved computing hardware.