
|
| 49-city USA tour; Newsweek, July 26, 1954 |
One of the first mathematicians to discuss the TSP was Harvard's Hassler Whitney, who presented the problem during a Princeton lecture in 1934. The TSP became known in the United States as the 48-states problem of Hassler Whitney, referring to the challenge of visiting each of the 48 state capitols in the shortest possible tour. (Alaska and Hawaii were not yet states at the time.)
In 1954, George Dantzig, Ray Fulkerson, and Selmer Johnson famously solved a slight variant of Whitney's problem, choosing a city in each state plus Washington, D.C. Not all of their cities were state capitols, since Dantzig wanted to use the table of road distances than accompanied his Rand McNally map.
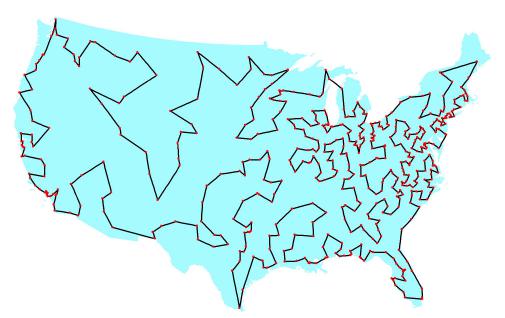
A much larger 48-states instance was solved by Manfred Padberg and Giovanni Rinaldi in 1987, making an optimal tour through 532 cities. This was a world-record solution at the time. The abstract to their research paper can be found here.
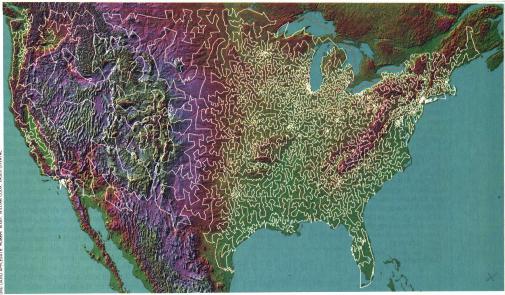
In 1998, Applegate et al. solved a 13,509-city USA instance. This example included every town and city in the contiguous 48 states having a population of 500 or more. This was again a new world record for the optimal solution of a test instance of the TSP. Information on the solution run can be found on the usa13509 page.

|
| 49-city USA tour; Newsweek, July 26, 1954 |
|
| 532-city USA tour; Padberg-Rinaldi 1987 |
|
| 13,509-city USA tour; Spektrum der Wissenschaft, April 1999 |